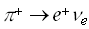was first discovered in 1958 and provided a confirmation of the V-A theory of weak interactions. Pion decays are weak processes which are theoretically calculable with high precision. In order to provide experimental information about pions three pion production facilities have been built worldwide, LAMPF (Los Alamos Meson Production Facility), TRIUMF (Tri-University Meson Facility), and one facility at PSI (Paul Scherrer Insitute), which produce pion beams of high intensities at low momenta.
Pions are spin zero bosons with negative parity; they form an isospin one multiplet with
where I3 is the third component of the isospin I. The charged pion has an average lifetime of [tau] p = 26.03 ns; its most probable decay mode is
,
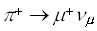(2.3)
with an average decay rate of
.
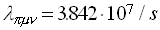The process called pion beta decay is the decay
,
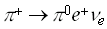(2.4)
with a p 0-meson and two leptons in the final state, thus a so called semileptonic decay. Since the pion beta decay is a transition between two members of an isospin triplet (2.2) it is analogous to super-allowed Fermi transitions in nuclear beta decay with
J p denoting spin J and parity p . At present, there are nine precise measurements of nuclear beta decay (a compilation is given in [Tow 95a]); one of them is the decay 14O to the first excited state of 14N [Cla 73]. The total decay energy of 14O is EF = 2.32 MeV and the decay rate is [lambda]F=0.00971/s. A rough estimation on the pion beta decay rate is obtained from the fifth-power law for beta decays
.
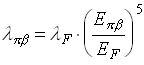(2.6)
With
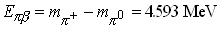one gets [lambda] p b ~ 0.3/s, which leads to the very
small branching ratio
Super-allowed Fermi transitions are pure vector interactions, since the axial vector contributions to the matrix elements of the transitions vanish due to spin and parity of initial and final states (Eq. 2.5). Experimental measurements of different super-allowed Fermi transitions show, that the product ft of the Fermi integral function f and the decay half life t is constant. This is explained by the CVC-Hypothesis, which postulates the conservation of the weak vector current. Following the CVC-Hypothesis, the ft values for super-allowed Fermi transitions are given by
where K is a product of fundamental constants (K = 8.1201·10-7). The uncorrected matrix element MF for transitions which fulfill (2.5) is
and the vector coupling constant GV can be expressed by
The Fermi coupling constant Gµ of pure leptonic decays
like
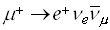is known with high precision from µ+ mean life
measurements. Vud is an element of the
Cabbibo-Kobayashi-Maskava (CKM) mixing matrix V
,
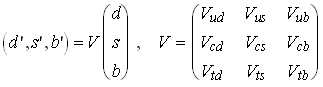(2.11)
where (d, s, b) are the mass eigenstates and (d', s', b') are the weak eigenstates of the quarks with charge -1/3. The unitarity of the CKM matrix V is tested most stringently in the top row
The unitarity, which must be satisfied if the Standard Model with 3 leptonic
generations is correct, is dominated by
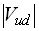~0.975.
The term
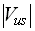is determined by analysis of semileptonic hyperon decays such as e.g.
;
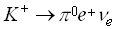its present value [PDG 94] is
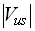~0.220.
The third term contributes only weakly to the sum in (2.12),
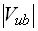~0.004.
In order to determine Vud from the nine accurately measured super-allowed Fermi transitions Eq. (2.8) has to be modified:
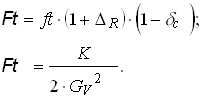(2.13)
Radiative corrections [Delta]R are composed of dominating, Z-independent parts and of Z-dependent terms of the order Z a 2 and Z2 a 3, where Z is the atomic number of the nucleus and a is the fine-structure constant ( a ~1/137). They are calculated for each of the nine mentioned transitions and amount to ~3.5% at most. The nuclear mismatch d c corrects the fact that isospin symmetry along the isomultiplet is violated by the coulomb and the nuclear force. The estimates on d c for the different nuclei are of the order of some tenth of a percent but have model dependent divergences [Wil 94]. A recent re-analysis [Tow 95b] , based on the newest Ft-values, leads to an unitarity test of
This result indicates a violation of the unitarity condition for the three generations by 2.1 standard deviations. Thus, the present determination of Vud from super-allowed Fermi transitions is not limited by the experimental accuracy with which the relevant ft-values are determined nor by the confidence on the various radiative corrections, but rather by the uncertainty of the nuclear mismatch d c.
Another independent determination of Vud comes from the decay of the neutron which does not require the d c correction but has the disadvantage of being a mixed vector-axial transition:
.
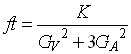(2.15)
The extraction of Vud requires therefore the knowledge of the neutron lifetime [tau]n as well as the knowledge of GA/GV, determined by the asymmetry in the emission of electrons from polarized neutrons; both of these measurements are very delicate.
From the mean lifetime of the neutron [tau]n=887.0±2.0 s together with the weighted average of the ratio GA/GV (the results are compiled in [Tow 95a]) individual values for the coupling constants can be deduced.
Again, the va
,
, (
.
,
.
.
.
(