




5.7 Simulated Photon and Positron Response of the CsI-Crystals
It was reported, that it is very important to understand the calorimeter
response to 70 MeV positrons and photons, since the number of
p b - and p ->e+ n e-events
below the p µe background needs to be estimated (see e.g. Fig
3.5). The response was simulated by use of the simulation package GEANT [GEA
94]. Monoenergetic positrons and photons of 70 MeV are directed into an
array of 26 crystals of the calorimeter (Fig. 5.11).
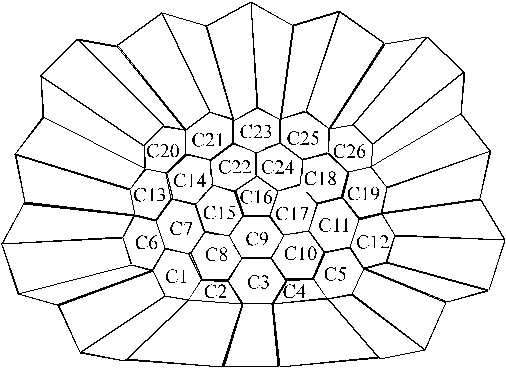 Figure
5.11:
The array of 26 crystals of the calorimeter as it is defined and positioned in
GEANT. Monoenergetic photons and positrons of 70 MeV are directed
from the origin into the crystals, uniformly distributed over their surface.
The properties and the types of the crystals are listed in Table 5.5.
The resulting energy spectrum of the calorimeter is displayed in
Fig. 5.12; one can see, that the two processes produce similar showers.
The tails are due to shower leakage at the front and the back side of the
detectors. The distributions are artificial, since they include only the effect
of electromagnetic showering.
Figure
5.11:
The array of 26 crystals of the calorimeter as it is defined and positioned in
GEANT. Monoenergetic photons and positrons of 70 MeV are directed
from the origin into the crystals, uniformly distributed over their surface.
The properties and the types of the crystals are listed in Table 5.5.
The resulting energy spectrum of the calorimeter is displayed in
Fig. 5.12; one can see, that the two processes produce similar showers.
The tails are due to shower leakage at the front and the back side of the
detectors. The distributions are artificial, since they include only the effect
of electromagnetic showering.
 Figure
5.12:
Simulated energy spectrum of the electromagnetic showers produced by
70 MeV photons (solid line) and positrons (dashed line) in the array of 26
crystals. The two distributions have almost identical shapes since a perfect
detector response is assumed.
In order to compare the simulated spectra to experimental data, properties of
the individual modules which affect the energy resolution of the calorimeter
are taken into account in the simulation: The resolution depends on the
photo-electron statistics and the light collection efficiency of the individual
crystals. The effect of light collection efficiency is incorporated in the
GEANT code in a subroutine (GUSTEP) which is called after each tracking step of
the electromagnetic shower. In this routine the deposited energy
(DESTEP) and the current position (x,y,z) inside the crystal
volume of any particle of the electromagnetic shower is recorded. The variable
DESTEP is multiplied by the current value of the function
flnu(z,r) (Eq. 5.9), which depends on the current
position of the secondary particle inside the crystal volume. After processing
one event, the energies dE(j) (j=1-26 denotes the crystal number)
deposited in each of the crystals, smeared by the optical uniformity function
flnu(z,r) are known. The parameters of the function
flnu(z,r) are the same for all crystals. The energies
dE(j) are then folded by a Gaussian function whose standard deviation
s (j) accounts for the effect of photoelectron statistics:
Figure
5.12:
Simulated energy spectrum of the electromagnetic showers produced by
70 MeV photons (solid line) and positrons (dashed line) in the array of 26
crystals. The two distributions have almost identical shapes since a perfect
detector response is assumed.
In order to compare the simulated spectra to experimental data, properties of
the individual modules which affect the energy resolution of the calorimeter
are taken into account in the simulation: The resolution depends on the
photo-electron statistics and the light collection efficiency of the individual
crystals. The effect of light collection efficiency is incorporated in the
GEANT code in a subroutine (GUSTEP) which is called after each tracking step of
the electromagnetic shower. In this routine the deposited energy
(DESTEP) and the current position (x,y,z) inside the crystal
volume of any particle of the electromagnetic shower is recorded. The variable
DESTEP is multiplied by the current value of the function
flnu(z,r) (Eq. 5.9), which depends on the current
position of the secondary particle inside the crystal volume. After processing
one event, the energies dE(j) (j=1-26 denotes the crystal number)
deposited in each of the crystals, smeared by the optical uniformity function
flnu(z,r) are known. The parameters of the function
flnu(z,r) are the same for all crystals. The energies
dE(j) are then folded by a Gaussian function whose standard deviation
s (j) accounts for the effect of photoelectron statistics:
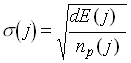 (5.13)
(5.13)
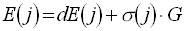 .
(5.14)
.
(5.14)
The number of photoelectrons per MeV, np(j), are the numbers
in Table 5.5 for each crystal, and G is a function that randomly
generates a Gaussian distribution of mean zero and standard deviation one. For
each event, the total energy Etot is calculated by summing
the energies deposited in the individual crystals:
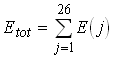 .
(5.15)
.
(5.15)
The resulting energy-spectra are displayed in Fig. 5.13. A difference between
showers initiated by photons and positrons occurs. It originates from the fact
that positrons interact close to the front face of the crystals, whereas
photons have a mean free path of about 3 cm in CsI; their showers thus are
shifted slightly along the crystal axis. As a result, the two types of showers
are weighted with different parts of the optical non-uniformity function
flnu(z,r).
The energy resolutions [Delta]E are obtained by fitting the distribution
with a gaussian function with exponential tail as defined in eq (6.16) in
section 6.4.1. They are [Delta]Ee=4.8 MeV (FWHM) for
positrons and [Delta]E g =6.0 MeV (FWHM) for
photons, respectively.
 Figure
5.13:
Simulated energy spectrum of the array of 26 crystals including the effects of
photoelectron statistics and optical non-uniformity. A difference between
showers initiated by 70 MeV photons (solid line) and 70 MeV positrons
(dashed line) can be observed caused by the light non-uniformity.
The simulated resolution for 70 MeV positrons and photons
([Delta]Ee and [Delta]E g ) are
depending on the parameters of the light non-uniformity function
flnu(z,r). The values of the parameters were chosen to
explain the differences found in the test experiments in 1994:
Figure
5.13:
Simulated energy spectrum of the array of 26 crystals including the effects of
photoelectron statistics and optical non-uniformity. A difference between
showers initiated by 70 MeV photons (solid line) and 70 MeV positrons
(dashed line) can be observed caused by the light non-uniformity.
The simulated resolution for 70 MeV positrons and photons
([Delta]Ee and [Delta]E g ) are
depending on the parameters of the light non-uniformity function
flnu(z,r). The values of the parameters were chosen to
explain the differences found in the test experiments in 1994:
* The energy resolution for a 70 MeV positron beam directed into the array
of 26 CsI presented in [Ass 95] is 4.2 MeV for the best crystal and between 4.9
and 5.6 MeV for typical crystals.
* A measurement of the calorimeter response to 70 MeV photons (see chapter 6)
leads to energy resolutions between 6 and 7 MeV for typical crystals.
For the final Monte-Carlo-Simulations it is desirable to extract the parameters
for flnu(z,r) from the tomography data itself, which makes
the simulation results even more reliable.
The numbers given for the energy resolution are mean values of the crystal
material available in 1994. With higher quality of the modules (better F/T
values, improved optical non-uniformity) the values will further improve.













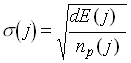 (5.13)
(5.13)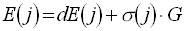 .
(5.14)
.
(5.14)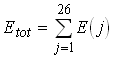 .
(5.15)
.
(5.15)




