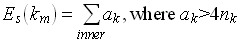1. Introduction to the pb Experiment - 6.3.4 TEMPERATURE CORRECTION AND GAIN MATCHING

6.3.4 TEMPERATURE CORRECTION AND GAIN MATCHING

The data acquisition runs were taken over a period of two days. The results of the individual runs have to be merged together and thus corrected for change in the light output due to the outside temperature fluctuations.

The temperature drift is determined by looking at the mean ADC-value of the individual runs as a function of time (Fig 6.8). The fluctuation is fitted by a polynomial of third degree. The ADC-values are then corrected on an event-by-event basis.

The total energy E_s, deposited for one event, is obtained by summing over all ADC-values a_k>4·n_k for the 14 inner crystals. The energy E_s is assigned to the crystal k_m with the maximum ADC-value a_max:

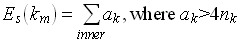. (6.14)

From E_s(k_m) the normalized energy E_n(k_m) is calculated according to equation 6.10.

Figure 6.8: Mean ADC-value of the events obtained from 10 runs (top) and mean temperature of the same period (bottom). For each event, the ADC-values of all crystals are summed after pedestal subtraction. The solid line is a fit with a polynomial of third degree. Gain matching corrects, first, the high voltage values of the PMT's which are not perfectly matched, and second, the drifts of the single PMT's. Again, gain matching is done in two iterations for each run, with initial values from the previous run.

The gain for each crystal is calculated from the requirement that the mean of the normalized energy spectrum of m events in one run is

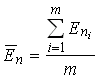= 66 MeV. (6.15)

Figure 6.9: Gain values for five crystals in the 14 analyzed runs. They are obtained by requiring the mean value of the energy spectrum to be 66 MeV. A clear mismatch of the HV -values is visible resulting in gain values ranging from 0.85 to 1.15. The run to run fluctuations are about 2%.. The statistical errors of the individual gain values are about 1%.. This value for is obtained from the simulation. The mean value and the resulting gain is calculated for each crystal. In order to decouple the gain matching from the influence of the gains of the neighboring crystals, only events with p>0.8 were used for gain matching, where p=a_max/E_s, i.e. events with more than 80% of the shower energy contained in one crystal. The resulting gain values are displayed in Fig. 6.9.

It is clearly visible that the gains of the PMT's for the six crystals of interest were not well matched, leading to gain correction factors between 0.85 and 1.2. The gain factors were calculated from the individual crystal spectra, which had low statistics. In order to avoid large statistical fluctuations, the new gain values were damped by 50% and calculated in two iterations for each run.