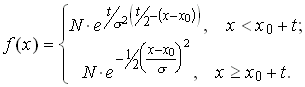1. Introduction to the pb Experiment - 6.4.1 EXPERIMENTAL RESULT

6.4.1 EXPERIMENTAL RESULT

The energy spectra of different sums of five crystals are displayed in Figure 6.10. The function used to fit the energy spectra is a gaussian with an exponential tail, which is continuos and differentiable at the transition point x₀+t:

(6.16)

The fit parameters displayed in the histograms are:

P1 = N, P2 = x₀, P3 = 2.355· s (= FWHM of gaussian), P4 = t. (6.17)

If parameter P4 is smaller than the s of the gaussian, the FWHM of the distribution is increased by the exponential tail:

Figure 6.10: Resulting energy spectra of the normalized energy E_n for different crystals sums. Top left: C9 and C16; top right: C9, C16 and C14; bottom left: C7, C9, C14, and C16 bottom right: C7, C9, C14,C16 and C22. The solid line is a fit to the data with a gauss-exponential function as defined in Eq. (6.16). The number in the lower left part of each graph is the FWHM (Eq. 6.18) calculated from the parameters P1-P4 of the fit. . 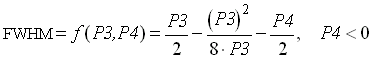( 6.18)

The FWHM values for the spectra in Fig. 6.10 are between 6.5 and 7.0 MeV.

The FWHM values for the individual crystal spectra are between 6 and 7 MeV. As can be seen from Table 5.5, the crystal C15, being at the center of the cluster, was returned to the manufacturer because of the low F/T-value. The energy resolution for this crystal (8.8 MeV) is much worse than the values obtained for the surrounding crystals. Therefore, events with C15 energies above 10 MeV are excluded in the summed energy spectra of Fig. 6.10.