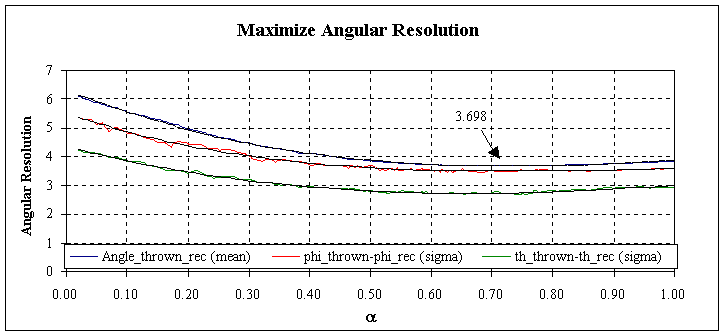
Angular Resolution
One of the goals of the analysis is the particle identification by cluster
recognition. In order to reconstruct the angle(s) of incidence I first
studied the angular resolution of our detector.
- A comparison of the positron and photon response at different energies
can be found here.
- Due to the size of the crystal's front face with an opening angle of
approximately 12 degrees you do not reach an uniform distribution of the
reconstructed vectors (Fig. 1). This one could get by changing a
down to ca. 0.3 but - as one can see by looking at g
- is due to a smearing of the angular resolution (Fig. 2). The black dots
mark the theta vs. Phi position for the reconstruction while the yellow
dots represent the thrown angles.
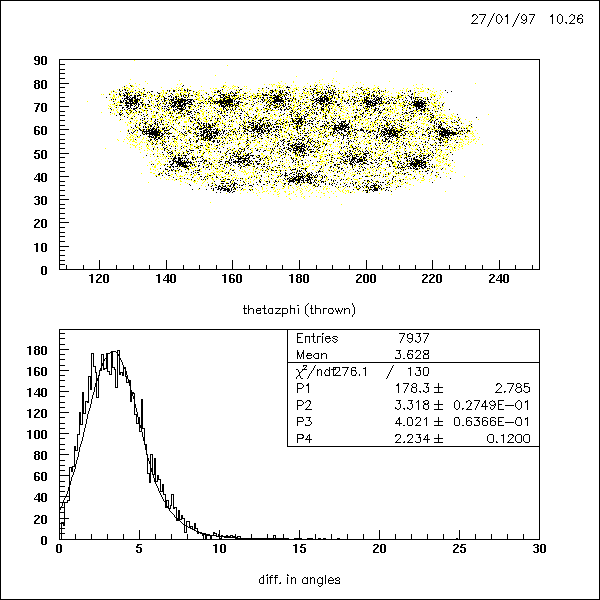
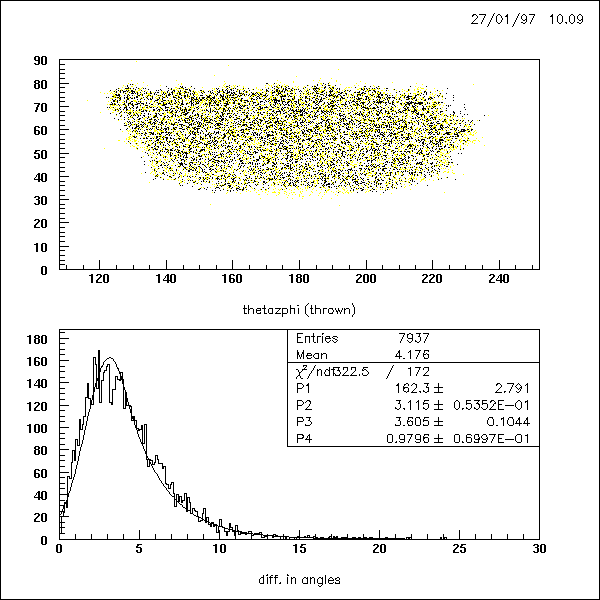
This has to be compared with the 'starting'-value a=1
; the number given in Ketevi's thesis was 5 degrees for the energy resolution.
(I am still puzzled why this figure is approximately 2 times better than
Ketevi obtained it. See page
158 of his thesis)
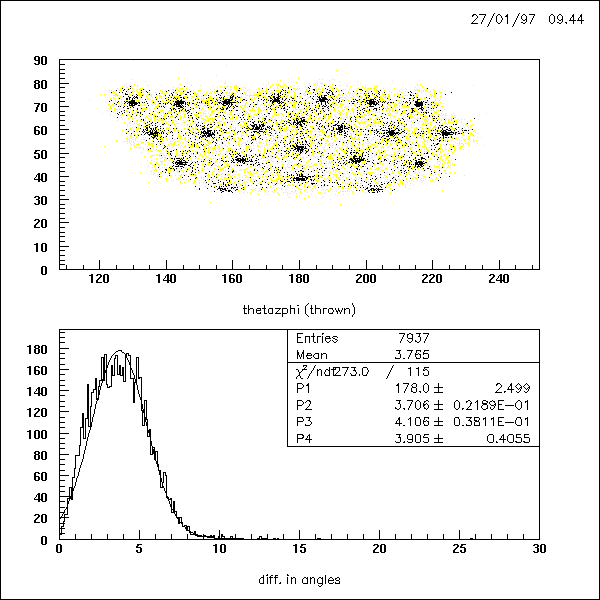
The main limit of obtaining a better angular resolution (besides the granularity)
are the shower fluctuations which lead to a large uncertainty of the reconstructed
position of incidence. This can be seen in the following picture where
I threw positrons exclusively to a point 5 degrees in phi right of the
center of the Pent. Without a weighting (or even more with a
>1 ) the spot looks smaller, but is completely off, since the position
of a crystal's center is overrated. Fig. 4 to 8 are showing the reconstructed
spot size and differences between thrown and reconstructed angles at different
weighting factors a.
a = 1 :
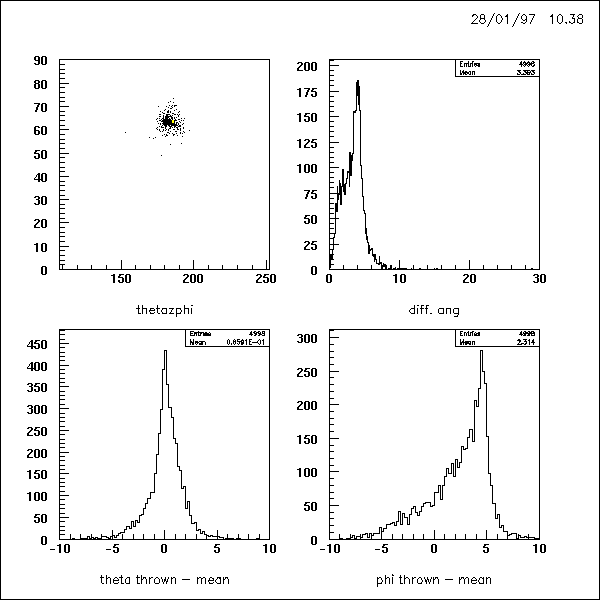
a = 3:
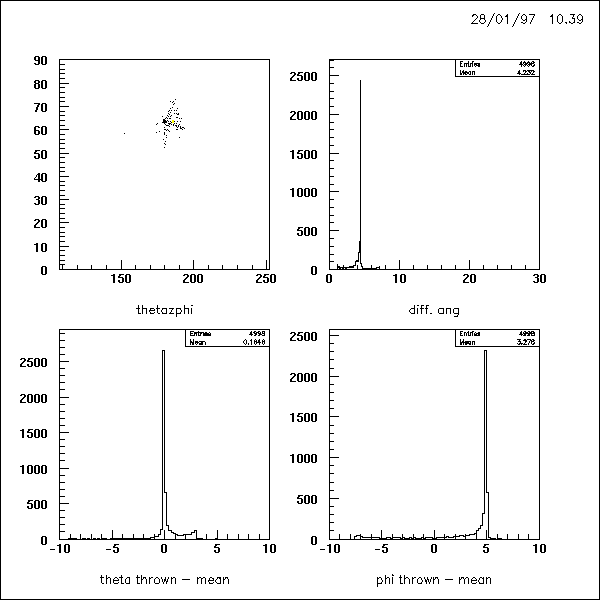
a = 0.71 :
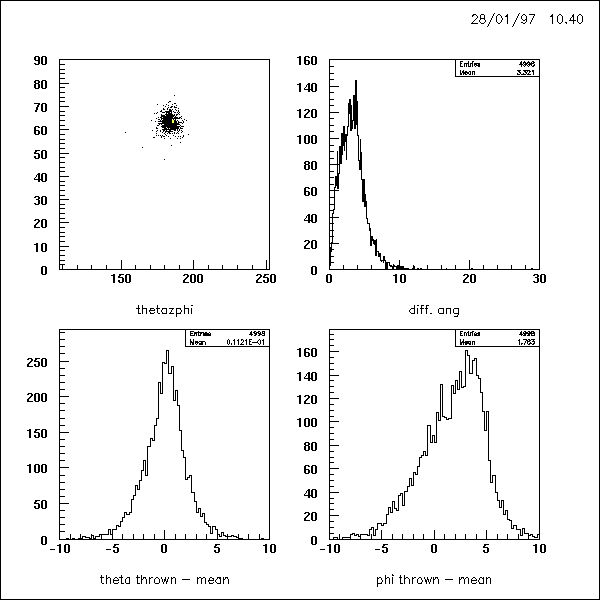
a = 0.43 :
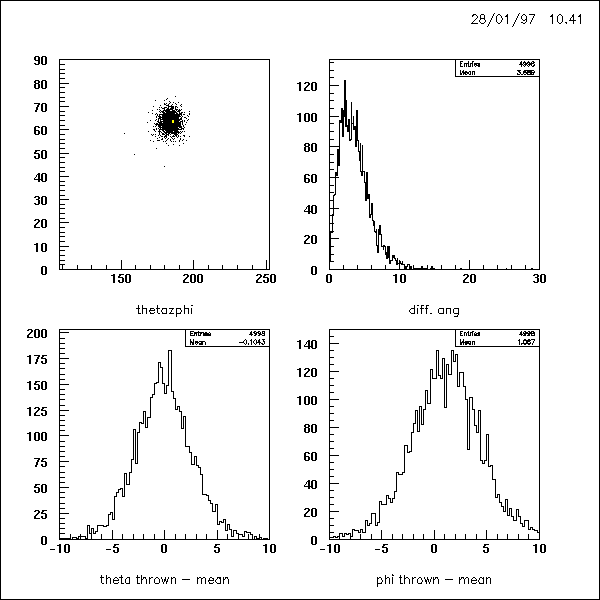
There is hardly a convenient way for a further improvement of the angular
resolution. Only if one could retrieve the exact appearance of the shower
and vary the weighting factor accordingly to the size/shape of the shower
and the crystals which were hit, a result of better than 3 degrees could
be expected.
Thomas Flügel
04-02-97
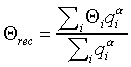
and had to be minimized by varying a. Looking
for the mean of the distribution of g, a
was found to be 0.71 .