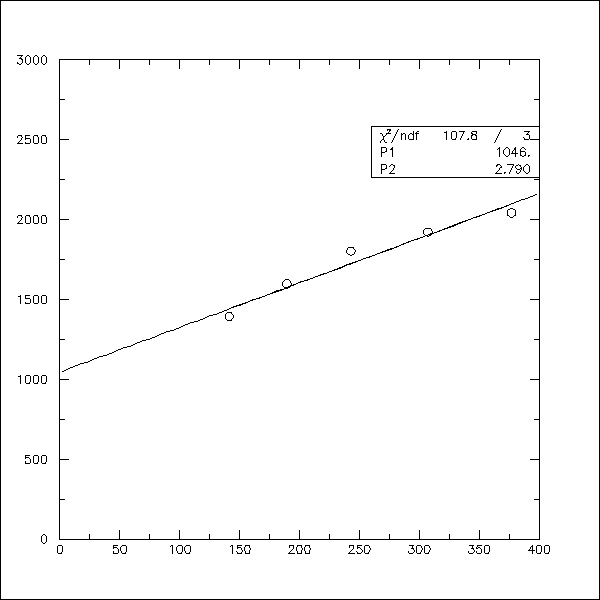Test of Cosmic Veto House Scintillator Material
Introduction
Several pieces of the scintillator
material to be used in the side walls of the cosmic veto house were tested
to determine their response to cosmic signals. The results are quoted
as the number of photoelectrons produced in a Burle Industries S83062E
1 inch photomultiplier tube per MeV of energy deposited in the scintillator.
Data and results can be found at the end of this page in Table 1.
Setup
The setup
was simple. All data was taken with the phototube coupled to the
end of the scintillator plank via airgap. The phototube anode was
maintained at a constant -1280 V. To collect cosmic data, a small
tagging detector was placed on either side of the plank about 1/3 of the
total length away from the phototube. This allowed us to collect
data from cosmics passing only through a small area of the scintillator
(~100 cm square). A simultaneos signal in the tagging detectors triggered
a 200 ns gate during which the signal from the phototube was integrated.
Event rates were roughly 0.75 Hz. The integrated signals of several
thousand events were binned into a histogram via ADC and the inhouse QVT
software. Data was also compiled for signals from a pulsed LED.
The 1 kHz driving pulse was split with one output triggering a 200 ns gate
and the other driving the LED (after proper attenuation to adjust the intensity
of the light). The LED was placed directly on the scintillator and
oriented perpendicular to the surface at the location of the tagging detectors.
LED Data was recorded exactly as the cosmic data; the signal from the phototube
being integrated while the gate was "on" and results recorded in a histogram.
Spectra for five different LED intensities were recorded. Figure
1 shows a typical pedestal corrected cosmic ray spectrum.
For comparison figure 2 shows cosmic data taken with a wavelength shifter
coupled to the scintillator via airgap and the phototube coupled to the
end of the wavelength shifter. Note that the distribution is shifted
towards zero but that the pedestal is still clearly distinct from the signal.
A typical LED spectrum is depicted in figure 3. The measurements
described above were repeated for each of nine different scintillator pieces.
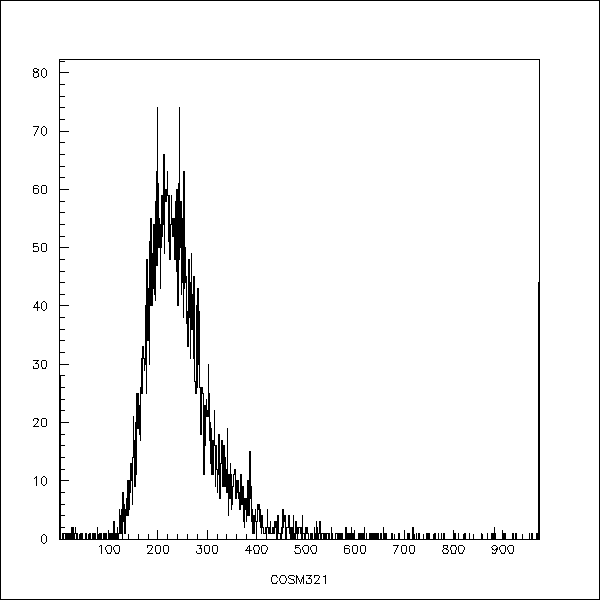
Fig.1 A typical cosmic event spectrum
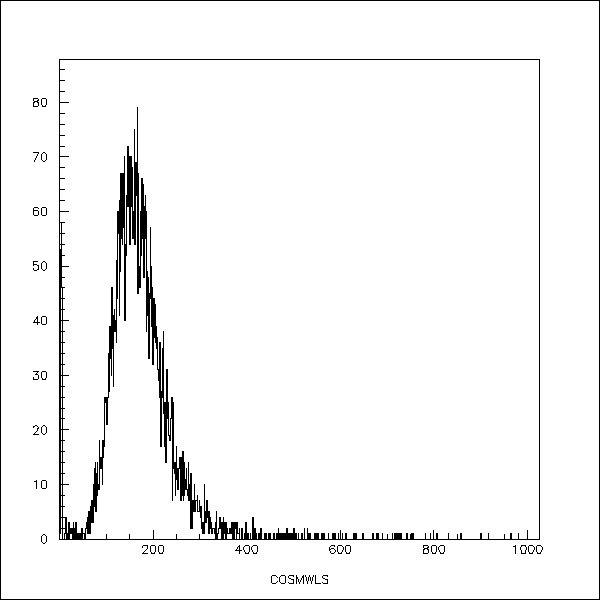
Fig. 2 Cosmic spectrum viewed through a wavelength shifter.
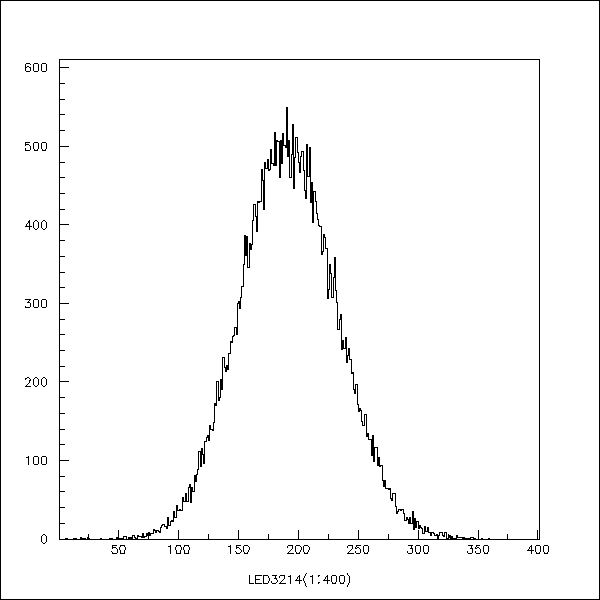
Fig. 3 A typical LED spectrum
Analysis
Data was analyzed via two different methods
yielding two significantly different results (see Table 1). Neither
method is entirely satisfactory and perhaps the results should be considered
as upper and lower bounds to the correct values. Evidently, the data
contains noise from an unknown source.
Gaussian Analysis
This data is typically analyzed by fitting
the LED data with gaussian functions (see figure 4) and plotting the squared
ratio of the mean position to sigma as a function of the mean position.
This data should form a line passing through the origin whose slope is
the number of photoelectrons per ADC channel. It can then be determined
how many photoelectrons correspond to the position of the mean of the cosmic
spectrum. Since the mean energy deposited by cosmic signals is known,
this in principle determines the number of photoelectrons per unit of energy
deposited in the scintillator. The width (sigma) of the distribution
has contributions from two sources. The first is the actual statistical
variation in the number of photoelectrons produced. It is this variation
which we wish to quantify. The second contribution comes from random
noise. This noise must be accounted for in the analysis. In
principle the random noise should remain constant throughout the experiment
such that the measured sigmas are all a constant amount greater than the
true statistical variation. Figure 5 shows a plot of sigma
squared versus the mean of the distribution for a typical piece of scintillator.
This data should form a line through the origin. The presence of
random noise of course shifts the y-intercept above the origin. There
is obviously an additional source of noise which is not constant.
Figure 6 shows the resulting plot of the squared ratio of the mean to the
corrected sigma. Note that the error bars on the data points (table
1) are again extremely small resulting in a very poor fit. Furthermore
the contribution of noise to the raw sigma used to compute these data points
is itself based on a poor fit (figure 5).
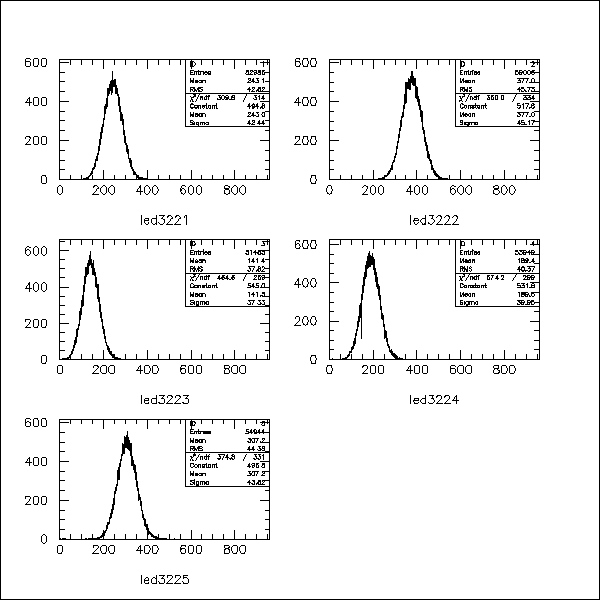
Fig. 4: data with gaussian fits for one scintillator
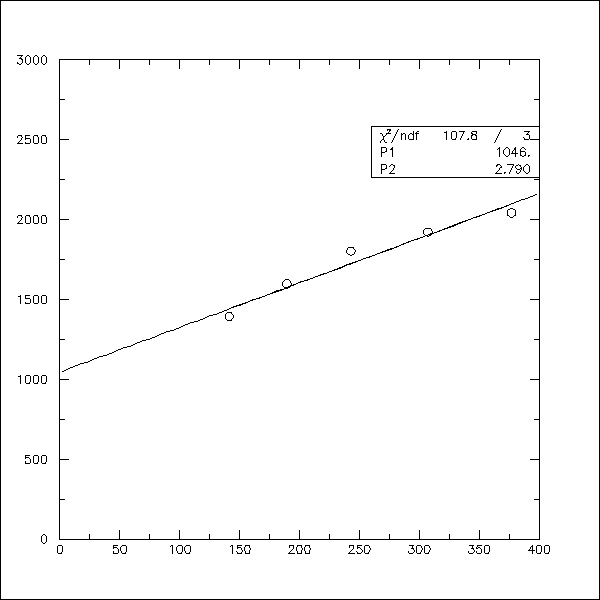
Fig. 5 (raw sigma)^2 versus mean for a single scintillator
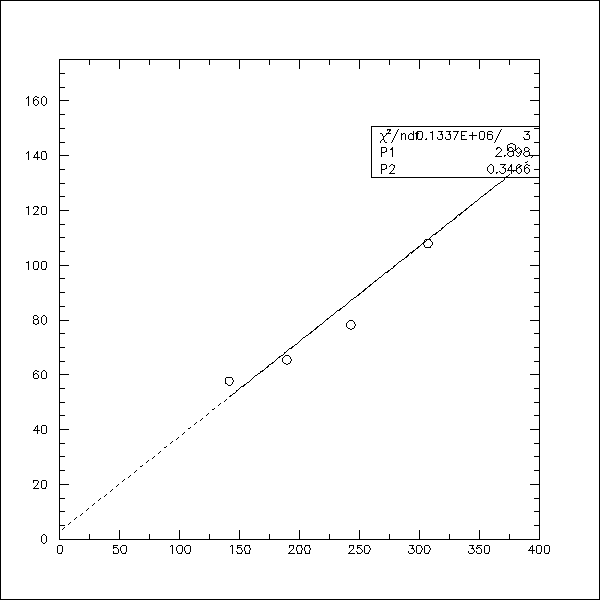
Fig.6 (mean/corrected sigma)^2 versus mean for a single scintillator.
A quick glance at Table 1 (and figure 4) shows
that the gaussian fits are quite good (chi^2/DOF ~ 1) and the statistical
errors on the fit parameters are very small. However, the linear
fits discussed above are very poor. As a solution to this problem
we keep only the three data points with the lowest means. The means
of the cosmic spectra are well contained within this range of means for
each scintillator and the three remaining points form a more reasonable
line (see Figure 7). The plots discussed so far display data
for a single scintillator plank (#322). Table 1 shows the complete
data and results from all tested planks. The final result for the
number of photoelectrons per MeV of energy is the mean of the results for
each individual piece and the error quoted is the statistical error in
the mean.
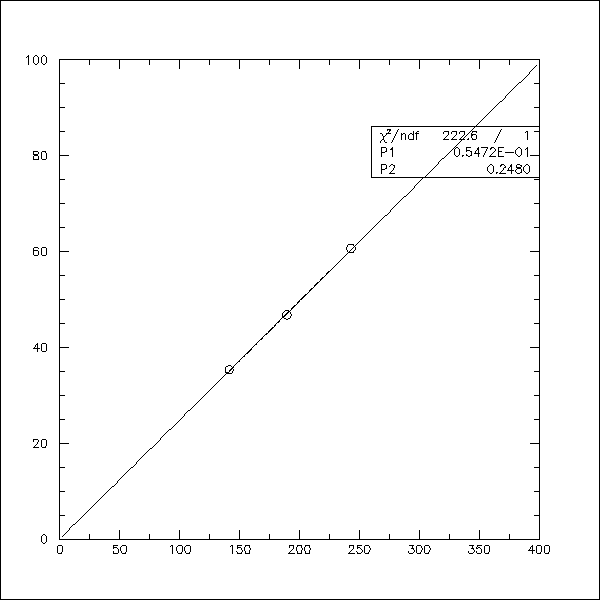
Fig. 7 (mean/corrected sigma)^2 versus mean
for only the 3 points with the lowest means.
Poisson Analysis
As an alternative
method of analysis we find the best fitting Poisson distribution for each
led spectrum (see figure 8). In this approach the fit parameters
are the number of ADC channels per photoelectron and the mean of the distribution.
This method clearly provides a more direct path to the desired result as
one of the fit parameters is the gain of the photomultiplier/ADC combination
and a close inspection of figure 9 reveals that Gaussian statistics may
be inappropriate anyway (note a slight asymmetry between the left and right
tails). The drawback to this method is that there is no way to account
for noise as with the Gaussian analysis.
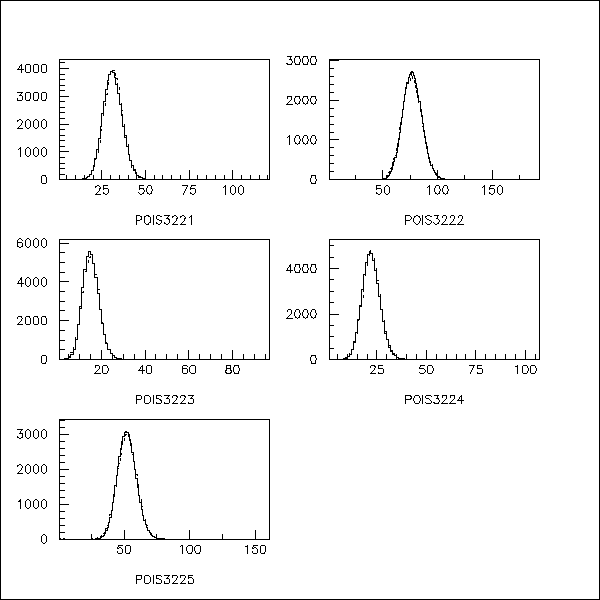
Fig 8 Led data and corresponding poisson fits (data in solid lines,
fits in dashes) for a single piece of scintillator. Note that the
scales are different since data must be rebinned to match the number of
ADC channels per photoelectron in the trial Poisson distribution.
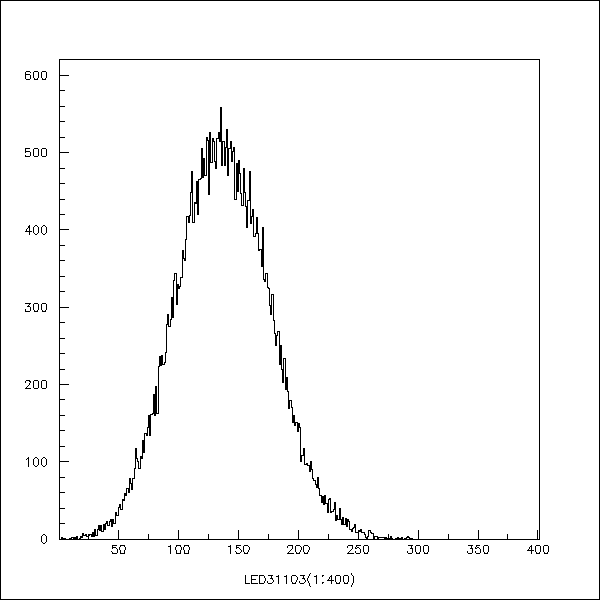
Fig. 9 As the intensity of LED pulses is decreased
the spectrum begins to deviate from a Gaussian
We obtained the number of
ADC channels per photoelectron from the fit of each LED spectrum.
This number is the fit parameter yielding the best value of chi^2.
Comparison with the corresponding cosmic distribution yields the number
of photoelectrons corresponding to the mean of the cosmic distribution
(measured in ADC channels). The dimensions of the scintillator and
dE/dx for cosmic muons in the scintillator material is known so that we
know the mean energy deposited in the material (~ 4.5 MeV). This
information allows one ultimately to compute the mean number of photoelectrons
produced in the phototube per MeV of energy deposited in the scintillator.
A value was computed for 5 data points in each of 9 planks and the results
averaged to give the final result (see table 1).
Scintillator Efficiency
The efficiency
of each scintillator piece was also computed. The efficiency is defined
as (signal events - pedestal events)/(total events) for cosmic data.
All pieces are more than 98% efficient.
|
|
Gaussian Fits |
|
|
|
|
Poisson Fits |
|
|
|
|
| Scintillator ID |
Cosmic mean |
mean |
sigma^2 |
chi^2 |
(mean/corrected sigma)^2 |
electrons/MeV |
ADC ch/e- |
chi^2 |
electrons/MeV |
|
|
| 000* |
416.17 |
158.62(0.18) |
1407.00(9.75) |
1.49 |
47.55(0.03) |
27.51 |
9 |
2.39 |
10.27 |
|
|
|
|
226.61(0.18) |
1643.49(10.50) |
1.11 |
64.72(0.04) |
|
8 |
2.02 |
11.56 |
|
|
|
|
258.04(0.19) |
1733.89(11.66) |
1.02 |
77.79(0.04) |
|
7 |
1.07 |
13.21 |
|
|
|
|
335.74(0.20) |
1904.45(12.22) |
2.20 |
109.81(0.05) |
|
6 |
1.10 |
15.41 |
|
|
|
|
516.10(0.20) |
2037.64(12.64) |
1.41 |
264.63(0.07) |
|
6 |
41.64 |
15.41 |
|
|
| 227 |
247.44 |
126.93(0.16) |
1327.14(8.01) |
4.09 |
35.12(0.02) |
14.77 |
11 |
4.12 |
5.00 |
|
|
|
|
171.15(0.18) |
1526.46(10.16) |
0.93 |
44.52(0.03) |
|
9 |
2.78 |
6.10 |
|
|
|
|
219.77(0.17) |
1663.82(10.60) |
1.42 |
60.73(0.04) |
|
8 |
1.44 |
6.87 |
|
|
|
|
281.35(0.19) |
1884.43(11.29) |
0.93 |
77.92(0.04) |
|
7 |
1.22 |
7.85 |
|
|
|
|
346.77(0.20) |
1998.98(12.52) |
0.99 |
106.37(0.05) |
|
6 |
1.09 |
9.16 |
|
|
| 228 |
239.38 |
147.01(0.16) |
1431.87(8.32) |
1.51 |
42.95(0.02) |
15.45 |
10 |
3.61 |
5.32 |
|
|
|
|
196.01(0.17) |
1612.02(10.44) |
0.94 |
56.23(0.03) |
|
8 |
2.53 |
6.65 |
|
|
|
|
252.93(0.18) |
1797.76(11.02) |
1.09 |
73.61(0.04) |
|
7 |
1.31 |
7.60 |
|
|
|
|
317.91(0.18) |
1940.40(11.45) |
1.08 |
99.90(0.04) |
|
6 |
1.62 |
8.87 |
|
|
|
|
390.54(0.16) |
2030.40(10.81) |
1.45 |
138.44(0.05) |
|
5 |
2.36 |
5.32 |
|
|
| 3110 |
241.97 |
136.32(0.17) |
1480.71(9.24) |
1.46 |
35.64(0.02) |
13.78 |
11 |
4.50 |
4.89 |
|
|
|
|
183.30(0.15) |
1694.97(9.06) |
1.30 |
45.67(0.02) |
|
10 |
4.45 |
5.38 |
|
|
|
|
237.16(0.19) |
1875.76(11.26) |
1.35 |
61.37(0.03) |
|
8 |
1.74 |
6.72 |
|
|
|
|
317.91(0.18) |
1940.40(11.45) |
1.08 |
103.01(0.04) |
|
7 |
1.53 |
7.68 |
|
|
|
|
370.44(0.19) |
2190.24(13.10) |
0.90 |
111.48(0.05) |
|
6 |
1.28 |
8.96 |
|
|
| 317 |
293.56 |
111.68(0.17) |
1329.33(8.75) |
2.54 |
21.89(0.02) |
12.37 |
13 |
4.07 |
5.02 |
|
|
|
|
152.04(0.17) |
1597.00(9.59) |
1.20 |
27.60(0.02) |
|
11 |
3.65 |
5.93 |
|
|
|
|
200.82(0.18) |
1802.85(11.04) |
2.42 |
38.66(0.03) |
|
9 |
2.98 |
7.25 |
|
|
|
|
317.91(0.18) |
1940.40(11.45) |
1.08 |
85.59(0.04) |
|
8 |
3.11 |
8.15 |
|
|
|
|
320.55(0.18) |
2202.43(12.20) |
1.25 |
71.22(0.04) |
|
7 |
2.03 |
9.32 |
|
|
| 321 |
252.14 |
142.99(0.16) |
1407.00(8.25) |
1.85 |
43.68(0.02) |
16.57 |
10 |
3.08 |
5.60 |
|
|
|
|
190.79(0.18) |
1615.24(10.45) |
1.13 |
53.82(0.03) |
|
9 |
2.00 |
6.23 |
|
|
|
|
246.25(0.18) |
1758.96(10.90) |
1.23 |
73.94(0.04) |
|
7 |
1.04 |
8.00 |
|
|
|
|
310.88(0.18) |
1936.00(11.44) |
1.09 |
96.93(0.04) |
|
6 |
1.50 |
9.34 |
|
|
|
|
381.58(0.19) |
2033.11(12.63) |
1.13 |
133.07(0.05) |
|
5 |
2.01 |
11.21 |
|
|
| 322 |
228.83 |
141.49(0.17) |
1393.53(8.96) |
1.73 |
35.33(0.03) |
12.62 |
10 |
3.63 |
5.09 |
|
|
|
|
189.58(0.17) |
1596.00(9.59) |
2.26 |
46.73(0.03) |
|
9 |
3.23 |
5.65 |
|
|
|
|
243.03(0.19) |
1801.15(11.03) |
0.99 |
60.62(0.04) |
|
8 |
2.06 |
6.36 |
|
|
|
|
307.17(0.19) |
1920.19(11.39) |
1.13 |
86.30(0.04) |
|
6 |
1.69 |
8.48 |
|
|
|
|
377.02(0.19) |
2040.33(11.74) |
1.05 |
117.14(0.05) |
|
5 |
2.43 |
10.17 |
|
|
| 7211 |
279.45 |
128.62(0.17) |
1445.66(9.15) |
1.58 |
35.63(0.02) |
16.33 |
12 |
4.11 |
7.76 |
|
|
|
|
177.42(0.17) |
1702.39(9.90) |
1.08 |
43.65(0.05) |
|
10 |
4.05 |
10.35 |
|
|
|
|
234.99(0.18) |
1854.16(10.33) |
1.32 |
63.26(0.04) |
|
8 |
2.97 |
8.87 |
|
|
|
|
301.70(0.18) |
2025.90(11.70) |
0.96 |
87.14(0.03) |
|
7 |
1.58 |
8.48 |
|
|
|
|
374.06(0.18) |
2092.15(11.89) |
1.53 |
125.96(0.03) |
|
6 |
2.09 |
5.18 |
|
|
| 729 |
334.85 |
114.04(0.17) |
1320.60(8.90) |
2.33 |
24.56(0.02) |
15.49 |
13 |
5.46 |
5.72 |
|
|
|
|
155.08(0.17) |
1569.74(9.48) |
1.18 |
30.89(0.03) |
|
10 |
3.48 |
7.44 |
|
|
|
|
203.67(0.19) |
1753.93(10.88) |
1.33 |
43.08(0.04) |
|
9 |
2.21 |
8.27 |
|
|
|
|
259.88(0.18) |
1939.52(11.47) |
1.15 |
58.81(0.04) |
|
8 |
2.33 |
9.30 |
|
|
|
|
323.85(0.18) |
2104.06(1.85) |
1.45 |
79.88(0.05) |
|
7 |
2.23 |
10.63 |
|
|
| average |
|
|
|
|
|
14.67(1.60) |
|
|
7.44(1.83) |
|
|
* Scintillator 000 was not included
in the averages as it was only half the width of the other board.