1.3.1 Nuclear beta decay

where g is related to the weak coupling constant and proportional to the value , M_fi is the nuclear matrix element, and F(Z',p) is the Fermi function. T_e and p refer to the kinetic energy of the decay electron and its momentum, respectively. The Fermi integral is defined as:

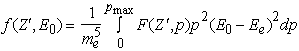
where E_o and p_max are the maximum available energy and momentum for the electron. In the limit that the emitted electron's mass is negligible with respect to its momentum, the ratio of these two values is a constant represented by:

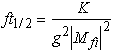
where 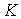is a constant. The value is only constant insofar as the matrix element 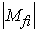is constant. For 0⁺ -> 0⁺ superallowed decays ([Delta]J=0, [Delta] p =0), this value is easily calculated:

where [tau] represents the isospin of the initial state nucleon. This, however, is not entirely accurate since it assumes that the initial and final states of the nucleus are pure isospin states. Nuclear and charge-dependent effects cause the isospin portion of the nuclear wavefunctions to be slightly mixed due to a presence of an isospin non-conserving term (INC) in the interaction Hamiltonian. This requires a correction to known as the nuclear mismatch. Additionally, radiative corrections must be applied due to the presence of electric charges. The modified value can thus be written,

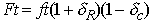
where (1 + d _R) represents the radiative corrections and (1 - d _C) represents the nuclear mismatch correction. The O(Z a ²) radiative corrections have been well documented ([Sir 87, Jau 87, Sir 86, Bar 92]). The nuclear mismatch correction is not well understood and is very model dependent as is illustrated in Table 1.2.

The pion beta decay process ( p ⁺ -> p ⁰ e⁺ n ) is a 0^- -> 0^- transition similar to the 0⁺ -> 0⁺ transitions in superallowed Fermi decays, with [Delta]J=0 and [Delta] p =0. No INC term exists for free pions that would require a nuclear mismatch correction d _C. This makes details of the pion beta decay process much less ambiguous with respect to nuclear beta decays and therefore provides a third method for testing the unitarity of the top row of the CKM. The present measurements of the pion beta decay rate yield a value of 1.025 ± 0.034 [PDG 96], with an uncertainty at a level of ~4% [McF 85]. This is not sufficient to test even the radiative corrections which are already at the level of ~3%.

According to the theory of conserved vector currents (CVC), the vector part of the weak current is not re-normalized by the strong force. The weak vector current is therefore the same in strength for muons, pions, and nucleons. The CVC hypothesis leads to a calculation of the pion beta decay rate of (1.0482 ± 0.0048) x 10^-8 with an Table 1.2: Values for the nuclear mismatch correction (in percent) for superallowed beta decays in several nuclei as calculated by various sources.

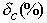
	[Bar 94]	[Orm 89]	[Har 90]	[Wil 90]	[Woo 91]	[Tow 95]
14O	0.12	0.19	0.28	0.32	0.33	0.22
26Alm	0.05	0.24	0.33	0.48	0.62	0.31
34Cl	0.11	0.48	0.64	0.84	0.98	0.61
38Km	0.10	0.49	0.70	0.90	0.91	0.62
42Sc	0.12	0.39	0.39	0.71	0.88	0.41
46V	0.05	0.21	0.45	0.65	0.89	0.41
50Mn	0.05	0.28	0.50	0.72	0.77	0.41
54Co	0.05	0.35	0.59	0.79	1.00	0.52

uncertainty of ~0.5% [McF 85].

1.3 Previous measurements

Several previous experiments involving precise measurements of pion decay rates have been performed. Most relevant to the pibeta project are those concerned with p -> e n ( g ) and p ⁺ -> p ⁰ e⁺ n ( g ) decays. Specifically, the recent p -> e n ( g ) measurements by G. Czapek et al. in 1993 and by D.I. Britton et al. in 1992 as well as the p ⁺ -> p ⁰ e⁺ n ( g ) measurements by W.K. McFarlane et al. in 1985 and P. Depommier et al. in 1968 are discussed in the following sections.