Initial Tests Of The Pion Beta Decay Detector

2.1 The weak force

The weak force is one of four fundamental forces in nature. A loose comparison of the relative strengths of these yields 10⁰:10^-2:10^-5:10^-39 for the strong, electromagnetic, weak, and gravitational forces respectively [Kra 88].This comparison becomes less accurate under certain circumstances. For example, the weak force is mediated by the massive W^±(~81 GeV), and Z^o (~93 GeV) particles. The propagator for these particles has the form:

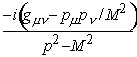
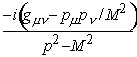
As p begins to approach the magnitude of the W and Z masses (), the weak force becomes comparable to the electromagnetic force [Ren 90]. However, for most situations (including the work described here) the momentum p is small relative to the mass of the W and Z and the weak propagator reduces to iG_Wg_{µ n} with G_W being a constant.

The weak force affects both leptons and quarks, although the quark eigenstates are different from those of the strong force as is discussed in section 2.2.

One of the difficulties which arises when trying to study weak interactions is the inevitable presence of electrically charged particles. In 1967 the Glashow-Salam-Weinberg (GSW) model unified the electromagnetic and weak forces into what are now referred to as electroweak interactions.The electroweak current can be expressed in the form:

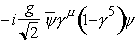
where 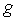is the weak coupling constant.

The presence of the (1 - g ⁵)in the electroweak current causes a tendency of weak decays to produce left-handed (negative helicity) particles and right-handed(positive helicity) anti-particles. To illustrate this, consider the operator:

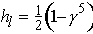
This is the left-handed spin projection operator for massless (or extremely relativistic) fermions. Starting with a Dirac spinor of the form:

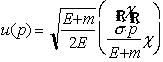
where the 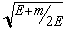normalization factor comes from requiring u^[dagger]u = 1.

Let the particle described by u(p) be traveling in the +z direction therefore making

and

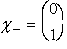
the two possibilities for [chi], corresponding to right and left handed helicity states, respectively. Using the Dirac-Pauli representation of the gamma matrices , g ⁵ is given by:

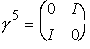
with I being the 2×2 identity matrix and 0 the 2×2 null matrix.

The expectation value of g ⁵ is then given by

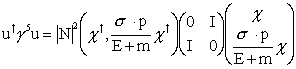
which yields

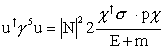
This gives an expectation value for h_l of

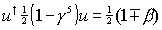
where b = v / c,and v is the velocity of the particle. The above equation demonstrates the relationship between the velocity and helicity of a fermion. In the limit of v = c, b = 1, and 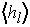becomes 1(0) for negative(positive) helicity particles as would be expected from a true projection operator. The presence of the (1 - g ⁵)therefore suppresses the coupling of electroweak currents of the "wrong" helicity in a very velocity-dependant way.