Initial Tests Of The Pion Beta Decay Detector - 2.3.1 Calculation of the [lambda]( p + -> p 0 e+ n ) / [lambda]([pi]+ -> µ+ n ) branching ratio

2.3.1 Calculation of the [lambda]( p + -> p 0 e+ n ) / [lambda]([pi]+ -> µ+ n ) branching ratio

A Feynman diagram of the p ^± -> l^± n decay process is shown in Figure 2.1 with l representing a lepton. The lepton current in Figure 2.1 can be written as

and the pion current can be written as .

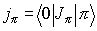Figure 2.1: Feynman diagram of a charged pion decaying into a lepton and a neutrino.

The pion current must be constructed out of the only available 4-momenta, q^µ = p_l^µ + p_n^µ, where p_l^µ and p_n^µ are the lepton and neutrino four-momenta respectively. This leads to a pion current of the form , yielding an invariant amplitude of

_{Simplifying then gives}

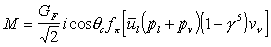
The Dirac equation can now be used to simplify the momenta into their respective particle masses yielding the matrix element

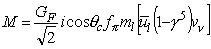
where the neutrino mass has been neglected.

Multiplying the invariant amplitude by its Hermitian conjugate and performing the appropriate spin sums yields

Evaluating the trace gives 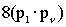. It is useful to write the dot product in terms of the lepton and neutrino energies only

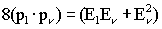
which then gives

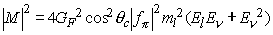_(2.3)

Now, using the common form for the decay rate of one particle into two particles yields

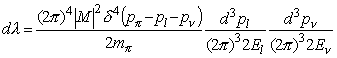
Using the three space components of the d ⁴-function, one can evaluate the integral over the "massive" lepton's momentum. In addition, since there is no angular dependence of the rate on the neutrino's direction, and since the neutrino momentum is equal to the energy, one can evaluate two dimensions of the integral over the neutrino's momentum and write the last variable of integration as the neutrino's energy.

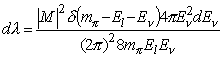
Before integrating, a change of variables ( y [equivalence] m_p - E_l - E_n )is made to simplify the argument of the d -function. When evaluating dy, it is tempting to say that since E_l = m_p - E_n, and thus dE_l = -dE_n. This, however, is incorrect because the d -function, technically, has not yet forced the energy conservation condition to be true. One therefore should write the "massive" lepton's energy as E_l [equivalence] (m_l² +E_n²)^½which uses the already present 3-momentum conservation condition yielding

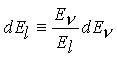
Making this change of variables and inserting the 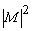from (2.3) gives

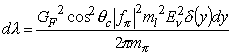
Integrating this is now trivial and allows the use of energy conservation to rewrite the neutrino energy in terms of the masses of the particles involved.

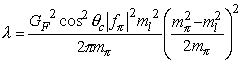
The ratio of the decay rates for the electron decay channel to the muon decay channel yields

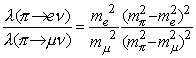
Inserting the appropriate masses, one obtains a value of 1.28 × 10^-4 for this ratio which is reasonably close to the currently accepted value of (1.230 ± 0.004) × 10^-4 [PDG 96].