The lepton current indicated in Figure 2.2 can be written as
while the pion current can be written as
Figure 2.2: Feynman diagram of the p ± -> p 0e±v decay process. The pion and lepton currents are indicated by j p and jl , respectively.
The exact form of the pion current is not easily derived. However, it must be constructed from the available 4-momenta. The pion current can thus be written in the general form
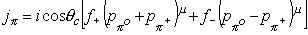
where p p + and p p 0 are the 4-momenta of the initial and final state pions respectively. The factor of (i cos q c) is included by convention with q c being the Cabbibo angle discussed in section 1.2. Considering the near symmetry of the pion masses and the small pion momenta involved, the f- term is negligible compared to the f+ term and will therefore be dropped.
Coupling the lepton and pion currents as described in section 2.3.1, an invariant amplitude of the form
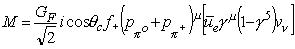
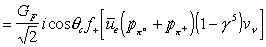
is obtained.
Again, considering that the pion mass is much greater than the pion momenta, the momentum terms can be neglected.
Multiplying by the Hermitian conjugate and performing the appropriate spin sums (i.e. summing over the initial and averaging over the final spin states) yields
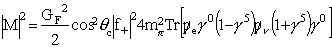
which simplifies to
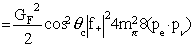(2.1)
where the charged and neutral pion masses have been considered to be the same. The three space components of the dot product would integrate to zero when calculating the decay rate so that only the EeE n term will contribute.
In general, the decay rate of the p -> p e n process is written
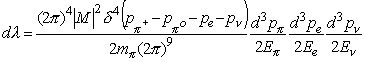
where p p +, p p 0, pe, and p n are the momenta of the initial state pion, and final state pion, electron, and neutrino, respectively. E p , Ee, and E n are the final state pion, electron, and neutrino energies, respectively. m p is the pion mass and M is the invariant amplitude defined in (2.1). The three space components of the d -function can be used to evaluate the integral over the final state pion momentum. The final state pion energy can be approximated by the pion mass m p . This yields:
where integration over two of the neutrino momentum components has been performed. The [Delta] represents the difference between the charged and neutral pion masses.
The d -function can now be used to evaluate the integral over the neutrino energy. Evaluating this integral and inserting the previously obtained expression for the invariant mass (2.1) yields:
where the electron mass has been neglected.
The total decay rate can now be found by performing the integration over the electron energy from 0 to [Delta].
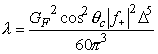
Finally, taking the ratio of this to the decay rate of the p ->µ n channel obtained in section 2.3.1 yields
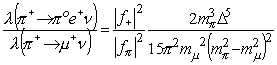
where the factors f+ and f p can be
assigned the values
and m p respectively. The f+ value can be
derived from observing that the pion current must contain an isospin lowering
(raising) operator for the decay of a p + (or p -)
which results in an eigenvalue of
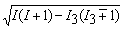which evaluates to
for I = 1 and I3 = ± 1. The value of
f p can be determined from the charged pion lifetime and
from GF (which is determined from muon decay).
f p comes out to be about 0.95 m p
[Ren 90]. Here, Halzen and Martin [Hal 84] is followed for
simplicity and a value of f p = m p is
used.
Inserting the appropriate values, one obtains for the pion beta decay branching ratio 1.009 × 10-8. The currently accepted value obtained from previous experiments is (1.025 ± 0.034) × 10-8 [PDG 96].