
where m is the electron mass,
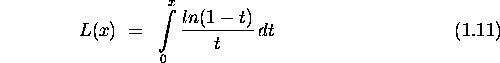
Integrating the Spence function from 0 to
The calculation of radiative corrections to the pion beta decay
rate can be taken from the nuclear independent radiative corrections
to ![]() transitions in nuclear beta decay. At
transitions in nuclear beta decay. At ![]() ,
these corrections neglect the strong interaction effects in nuclear
beta decay, and can be applied to the purely weak pion beta decay.
This radiative correction function is based on a function
,
these corrections neglect the strong interaction effects in nuclear
beta decay, and can be applied to the purely weak pion beta decay.
This radiative correction function is based on a function
![]() which has been derived by Sirlin [12], and
takes the form
which has been derived by Sirlin [12], and
takes the form

where m is the electron mass, ![]() is the electron end-point
energy, p is the electron momentum,
is the electron end-point
energy, p is the electron momentum, ![]() , and L(x) is the
Spence function:
, and L(x) is the
Spence function:
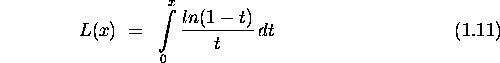
Integrating the Spence function from 0 to ![]() ,
one obtains L=-1.5934.
,
one obtains L=-1.5934.
When applied to pion beta decay and averaged over the electron spectrum,
the function ![]() becomes [18]
becomes [18]
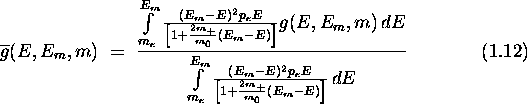
where ![]() is the
is the ![]() mass and
mass and ![]() is the
is the ![]() mass.
To a good approximation, the denominator is found to be
mass.
To a good approximation, the denominator is found to be
![]() [12].
[12].
Integrating the numerators numerically over the electron energy, one
obtains ![]() . This can be compared with the
asymptotic result for large
. This can be compared with the
asymptotic result for large ![]() , which neglects recoil [18],
, which neglects recoil [18],
![]()
The radiative correction is derived by Marciano and
Sirlin [13] and takes the form
![]()
where ![]() is a QED short-distance enhancement factor equal
to 1.02256, and
is a QED short-distance enhancement factor equal
to 1.02256, and ![]() is a running QED coupling which satisfies
is a running QED coupling which satisfies
![]()
such that ![]() and
and
![]() .
. ![]() is a small perturbative QCD
correction estimated to be -0.34, and C is a nuclear
structure-dependent correction which is 0 for
is a small perturbative QCD
correction estimated to be -0.34, and C is a nuclear
structure-dependent correction which is 0 for ![]() transitions.
transitions. ![]() is a low energy cutoff applied to the
short-distance part of the
is a low energy cutoff applied to the
short-distance part of the ![]() box diagram, and ranges from
400 MeV to 1600 MeV. Using this range of
box diagram, and ranges from
400 MeV to 1600 MeV. Using this range of ![]() , the radiative
correction to superallowed
, the radiative
correction to superallowed ![]() Fermi transition rates is
found to be between 1.0334 and 1.0350. [13]
Fermi transition rates is
found to be between 1.0334 and 1.0350. [13]