Because the positive and neutral pions are members of an isospin multiplet,
it is possible to describe them mathematically with the ladder operators in
isospin space. The ladder operators take the form
where 
(
) is the absorption (emission)
operator for the neutral pion, and 
() are the absorption (emission) operators for the
charged pions.
Applying the operator 
to a state with one pion with
a given charge produces another state with a pion of the same momentum but
with the charge increased by one unit. [9]
Using the isospin ladder operator formalism, the vector part of the interaction
for nuclear beta decay [9] becomes:
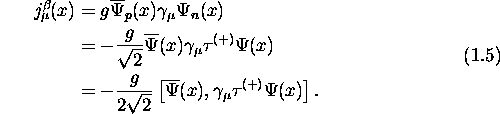
If one compares Equ. 1.5 with the electromagnetic current of a nucleon
system, which takes the form
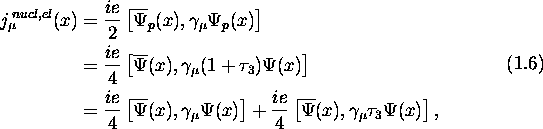
it is apparent that the second term in Equ. 1.6 can be understood as
another component of the nuclear beta decay vector current in Equ. 1.5.
For further clarification, the vector current from Equ. 1.5 may be
written as
Upon further study of Equ. 1.6, one finds that the electromagnetic
current of the nucleon system is not a conserved quantity [9]. However,
if one adds another term corresponding to the pion electromagnetic current, a
continuity equation is created:
Because this added term for the pion electromagnetic current can be shown to
have only an isotopic vector part [9], the continuity
equation 1.8 can be written as
where 
is the isotopic scalar part of the
nucleon system electromagnetic current, and
is one component of the
appropriate vector electromagnetic current.
In order to be invariant under rotations in isospin space, each of the two
terms in Equ. 1.9 must be conserved separately. Consequently, each
component of the vector term must also be conserved. Hence, the following
conservation law must be true:
The addition of the pion electromagnetic current term in Equ. 1.8,
which results in the conservation law of Equ. 1.10, has implications for
the form of the beta decay electromagnetic vector current given in
Equ. 1.5. Specifically, in order to explain the apparent equality
of the weak interaction vector coupling constants 
in nuclear beta decay and
in muon decay, a corresponding pion electromagnetic current term should be added to
the beta decay nucleon electromagnetic current in Equ. 1.5.
This added term in the expression for 
implies the existence of a new contribution to the weak interaction Hamiltonian.
The new contribution drives the beta decay of the pion,
or 
. [9] By measuring
the pion beta decay rate precisely, and comparing it with the theoretical value
obtained from the modified weak Hamiltonian, one can determine whether the CVC
hypothesis is true.