,
, 
, 
, and 
are the momenta of the negative pion, proton,
neutral pion, and neutron, respectively. Assuming that the pionic hydrogen 
atoms are at rest, and solving for the energies 
and 
of the 
and
the neutron in the lab frame,
one finds
, and
, 
, 
, and 
are the masses of the negative pion, proton,
neutron, and neutral pion, respectively. 
is the mean binding energy of
the pionic hydrogren, and is equal to -0.37
0.08 keV. [6]
In the rest (primed) frame of the , the 
decay produces
two anticollinear photons, as shown in Fig. 1.1. In order to calculate
the momenta of the photons in the lab frame, one must perform the appropriate
transformation. For this purpose, the momentum of the in the lab (unprimed)
frame is defined to be in the x direction. Consequently, the boost from the
primed frame to the lab frame is along the negative x direction, as shown in
Fig. 1.1.
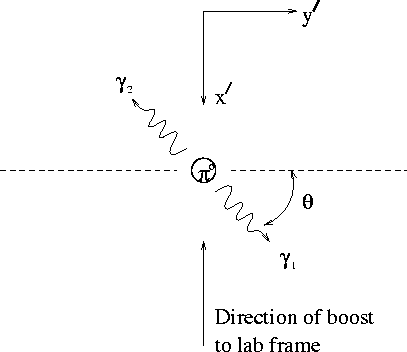
Figure 1.1: Decay of a neutral pion into two photons, in the rest (primed) frame of
the pion.
In the primed frame, the four-momenta of the two photons take the form:
where 
MeV.
Transforming to the lab (unprimed) frame with a boost in the negative x direction
for 
,
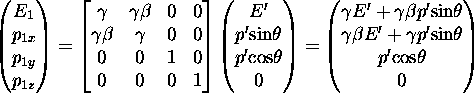
and
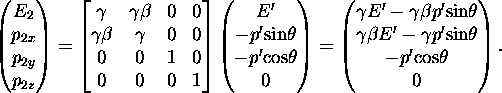
From the above expressions for 
and 
in the lab frame, one
can see that the energy and momenta of the two photons are completely
determined by the angle 
in the primed frame. Because the
probability of values for the angle is uniform from 0
to 180, the spectrum of energies for the two photons forms
a flat ``box'' spectrum, ranging from the minimum to the maximum
allowed values.
The relative
angle 
between the two photons can be calculated from the general
formula for the angle 
between two vectors A and B,
As a result, the expression for takes the form
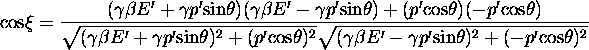
Finally, the energy of one photon in the lab frame is plotted against
in Fig. 1.2. From the graph, one can see that the photon energies
in the lab frame range from 54.9 MeV to 83.0 MeV.
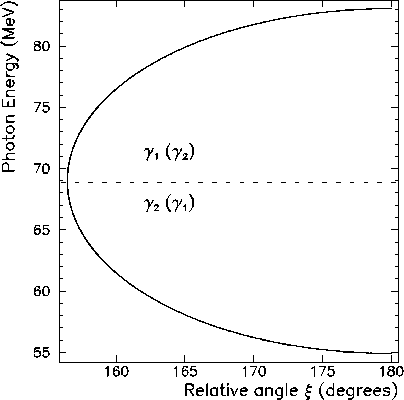
Figure 1.2: Energy spectrum for photons from the decay
plotted against the relative angle between the two photons, all in the lab
frame.