The Pion Beta Decay Experiment and A Remeasurement of the Panofsky Ratio

7.6 Photon Spectrum and Fit

After applying the above described cuts, a clean spectrum with two well-separated distributions emerged. The two peaks were fitted separately and the area under the peak was calculated as seen in Figure 7-15. The local minimum at 80.9 MeV was chosen as the separation limit between RC- and SCX- events. The RC-peak follows a Gaussian+exponential shape due to a (1-e) like energy loss, as experienced in previous measurements using beam positrons and tagged photons [Bro96]. The theoretical distribution for SCX photons would be a box graph. Thus the left tail also was approximated by an exponential curve, while the right tail follows a Gaussian shape. This has been visualized by adding the simulated response to monoenergetic photons between 55 MeV and 83 MeV. This intermediate section best could be fitted with a parabola.

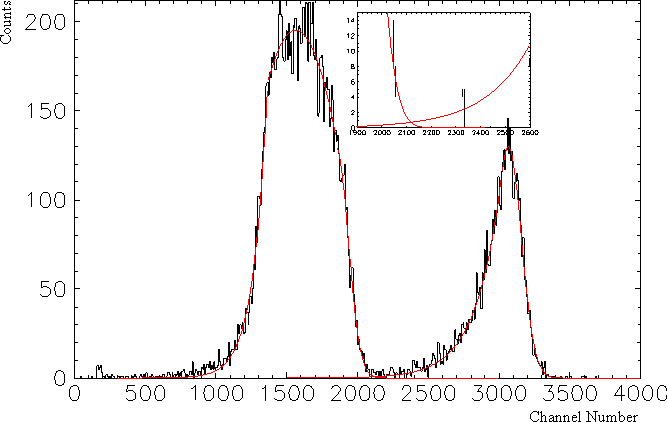
Finally, for the fit of both measured and simulated response to SCX photons, three subsections were pre-fitted using the above reported functions to obtain the starting values for the final fit. Then a function comprising the exponential curve, parabola and Gaussian with a total of 8 parameters was generated and fitted to the spectra using the MINUIT routine [PAW96]. The accuracy of this fit was determined with the fit errors calculated by MINUIT. The precision for the determination of the area under the fit function was 0.2%. The tails of the fit functions also were used to estimate the RC content under the SCX distribution. Thanks to the clean cuts using the outer ring the low energy tail of the RC-peak has no more than 0.3% of its entries below 90 MeV. Due to the good energy resolution and the cut on the neutrons, the SCX distribution's right tail only contributes with 4*10^-4 per cent to the RC peak. As the left tail is concerned, unidentified low energy background, i.e. due to cut inefficiencies, was excluded owing to the fit function.

Figure 7-15 Typical data sample (from Run403) superimposed by the individual fit-functions (see text). The excerpt focuses the overlapping region and demonstrates a low contribution of each peak to the other.

In order to account for the influence of detector geometry and cuts for the determination of the Panofsky rate the detector acceptance was determined using the GEANT simulation and fit functions described above. An acceptance correction of 1.0327±0.42% was obtained.

The final result after summing the individual data runs amounts to

1.5986/1.0327*0.999 ± (0.27% 0.65%) = 1.546 ± 0.010.

The statistical error of 0.27% comprises 0.17% error from data and 0.10% from simulation. The systematical error is mainly caused by the uncertainty due the cuts and differences between simulated and measured spectra. Thus an improved accuracy for Panofsky ratio could not be achieved. Nevertheless the obtained value for P is in good agreement with the previous measurements [Spu77] and theory [Pan76]. A further discussion of the result will be given in the subsequent section.