Analysis of the pi- p -> p0 n data

Introduction

During our beam time in July/August 1994 we did several tests to calibrate the pure CsI crystals. In order to test the response of the crystals to 70 MeV gammas, negative pions were stopped in a liquid hydrogen target. A fraction of ca. 60% of the pi- p atoms undergo the charge exchange reaction pi- p -> p0 n. Due to the kinetic energy of the pi0, the energies of the 2 gammas from the pi0-decay are between 56MeV and 84MeV. Showers in the crystals initiated by such gammas were used to calibrate our array of 26 CsI crystals (Fig 1).

Method of the calibration

A schematic diagram of the charge exchange reaction and the terms used in the following is shown in Fig 2, Fig 2 EPS. By measuring the angle between the neutron and the gamma1 (theta_1n), one can calculate the energy of the gamma 2 and compare it with the energy deposited in the CsI array:

Fig 3 EPS

The setup (Fig 4), (Fig 4 EPS) for this experiment is determined by the above method. The neutron counter consists of 30 plastic scintillator plates, the tag detectors are 12 pure CsI crystals of type HD1, HD2. The energies of gammas from valid events (neutron and 2 gammas detected) are lying between 68 and 75 MeV (red lines in Fig 3).

Simulation

In order to normalize the experimental data, the kinematics of the decay and the experimental setup was put in a Monte Carlo Simulation: The stopping distribution in the LH2-taget of +/-5cm in beam direction and +/-1cm perpendicular to the beam was taken into account as well as the position and the geometrys of all the detectors. The angular resolution of the setup results in a energy resolution with a FWHM of ~0.7MeV (Fig 5), (Fig 5 EPS).

The total uncertainty from the positions of the neutron and the tag detectors in space for is s_th~2deg=0.035rad. The corresponding energy uncertainty s_E is at most: s_E =16MeV*s_th = ~0.6MeV. The geometrical position of the CsI crystals in space is not as well known, since the crystals where enclosed in a big, light-tight box. Therefore, only the positions of the sides and the front wall could be measured, which does not lead to a precise location of the CsI crystals. Two methods were used to correct the CsI array positions:

(1) By comparing the simulation rates and the experimental rates in the individual crystals.

(2)The momentum vector p_g2 (see Fig. 2) of the gamma2 is computed for each event out of the neutron and tag position. This vector is then compared with the C.M. vector of the shower for that particular event:

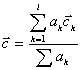
where c_k is the unit vector pointing to the center of crystal k with ADC value a_k. By switching to spherical coordinates:

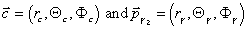
the difference in polar (theta) and azimutal (phi) angle can be calculated.

The angular resolution of the CsI array can be determined by cutting on individual tag and CsI counters. In Fig 7 top left, right, and bottom left are the difference in polar (theta) and azimutal (phi) angle for crystal C7 and tag counter T7. Bottom left is the total angle between the two vectors (caculated with the scalar product). This histogram could be interpreted as the angular resolution of the CsI array, which is therefore ca. 3 deg.

Fig 8 shows delta_theta for cuts on individual tag counters. The double peaks can be resolved by cutting on the different crystals (Fig 9) . Systematic shifts are observed, eg. d_th C15 is centered for T10 and moves to left for T11, T12.

Results of the experimental data

In order to give an idea, how the experimental data were analysed, a short description of the analysis routine follows.

Pedestal substraction

Two effects must be distinguished: 1) The pedestal and noise of an ADC channel, which is depending on the PM and the whole electronics, including splitter, ADC etc. for that particular channel and 2) the common mode, which is a common noise affecting all the channels simultainously. The common mode value is calculated by summing over all the channels, but distinguished by the two PM-types that were used. The modules, that surround the crystal with the maximum ADC value, i.e. which has been hit by a gamma, are excluded for common mode calculation. Fig 10, Fig 10 EPS shows the common mode for the EMI 9821 Q PM's with CERN bases (left) and the EMI 9822 QB PM's with UVA bases(right).

After common mode substraction, the pedestal value of each channel is determined by summing over the events of one run in the first iteration:

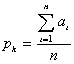, where p_k = pedestal of channel k, a_i = adc value for event i of channel k, n = number of events. This pedestal value is then substracted in the second analysis iteration. The noise n_k in each channel is defined as:

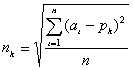, where n_k is the noise in channel k. Fig 11, Fig 11 EPS shows the remaining pedestals after two iterations (left) and noise (right) for run166.

Gain matching and temperature correction

Temperature correction is a common correction for all the crystals due to the temperature change in the box during the data taking. It is determined by looking at the mean of the 70MeV peak of all the crystals as a function of time. The drift of the peak during one night of data taking was about 3% and is corrected on a event by event basis. (Fig 12)

The total energy deposited E_s for one event is obtained by summing over all ADC values >0 and is assigned to the crystal with the maximum ADC value. The theoretical energy E_g2 of the particular event is calculated from the tag and the neutron counter hit. The normalized energy E_n is thus: E_n = E_s/E_g2*70.

Gain matching corrects high voltages for the individual PM's, that were not perfectly matched. It is done in two iterations for each run, with starting values from the previous run. The gains are determined on condition that the mean of the normalized energy E_n of the spectrum of each crystal is at 70 MeV. In order to decouple the gain matching result from the influence of the gains of the neighbouring crystals, only events with p>0.8 were used for gain matching, where p= ADC_max/E_s, i.e. events with more than 80% of the shower-energy contained in one crystal.

Resulting Spectra

Figure 13 shows the Theta-Phi projection of the c.m. of hits on the frontface of the crystals (green) and the calculated vectors from tag and neutron detectors (red).

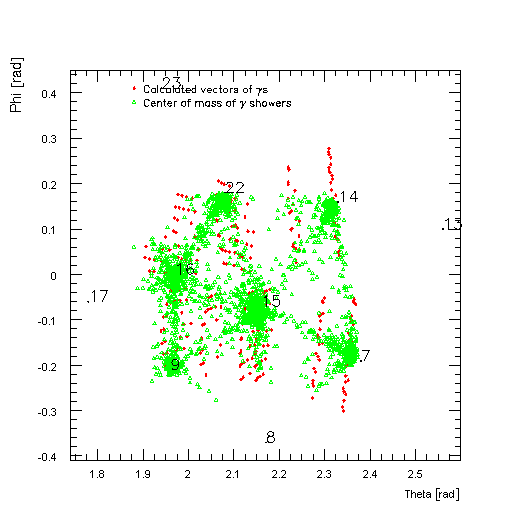
Fig 13 PostScript, Fig 13 separated PostScript

The function used to fit the resulting spectra is a gauss-exponential function which is steady and differentiable at the transition x0 + t. The total width FWHM TOT is a function of the parameters P3 and P4.

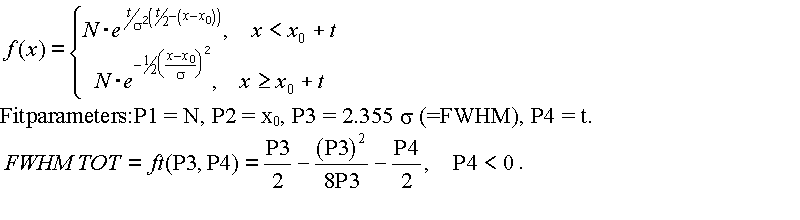
The statistical error m_ft of the FWHM TOT is calculated using the error matrix for the fit obtained from MINUIT and using the gaussian error propagation law:

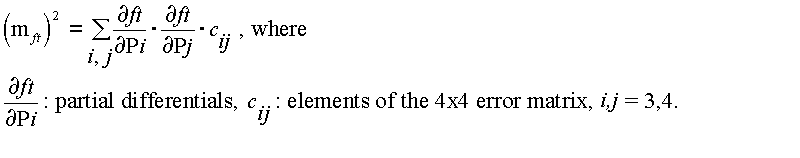
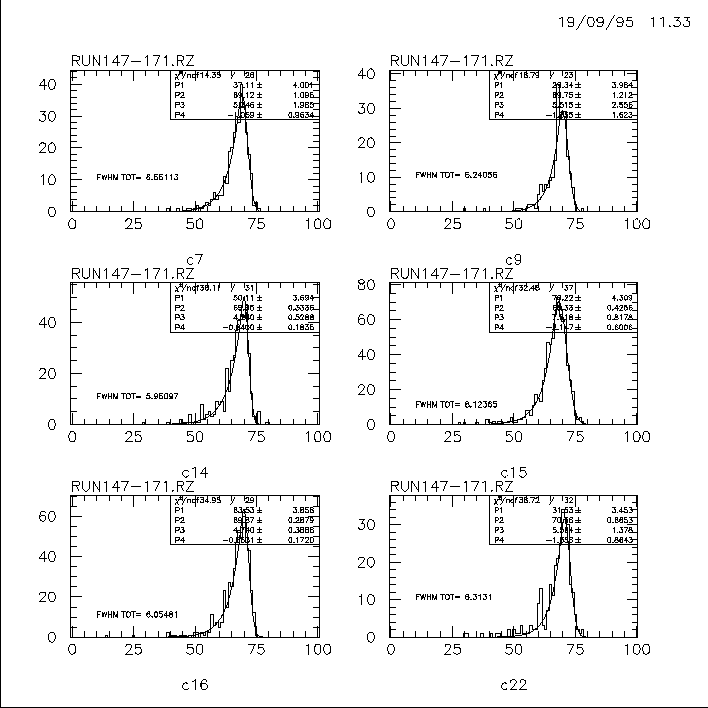
The resulting spectra are and their fitting parameters are (FIG 14):

Fig 14 PostScript

A compilation of the results obtained above:

Crystal Nr.	Peak[MeV]	FWHM Tot[MeV]	FWHM Tot[%]  	
C7		69.1		6.6+/-0.2	9.5		
C9		69.8		6.2+/-0.3	8.9			
C14		70.5		6.0+/-0.2	8.5
C15		68.3		8.1		11.8
C16		69.9		6.1+/-0.3	8.7
C22		70.6		6.3+/-0.3	8.9

Adding the above spectras leads to (Fig 15):

Fig 15 PostScript

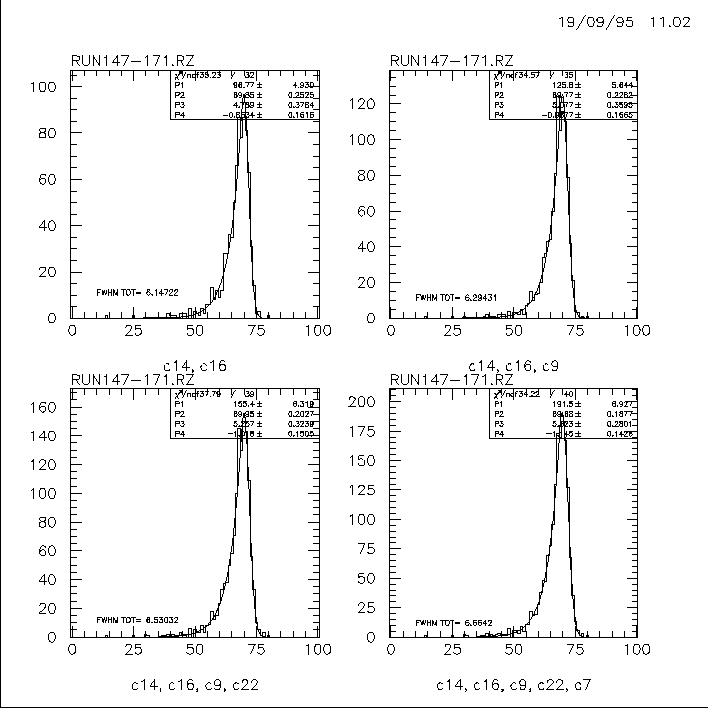
The results for the summed spectra:


Crystal Nr.	Peak[MeV]	FWHM Tot[MeV]	FWHM Tot[%]  	
C14,16		69.9+/-0.2		6.2+/-0.06	8.9		
C14,16,9	69.8+/-0.2		6.3+/-0.06	9.0			
C14,16,9,22	70.0+/-0.2		6.5+/-0.05	9.3
C14,16,9,22,7	69.7+/-0.2		6.7+/-0.04	9.6

Crystal C15 has not been added, since it is clearly worse than the rest of the crystals for two reason: It is a russian crystal with bad FT-value, and its high voltage was 30V under the value obtained by gain matching with 70 meV e+.

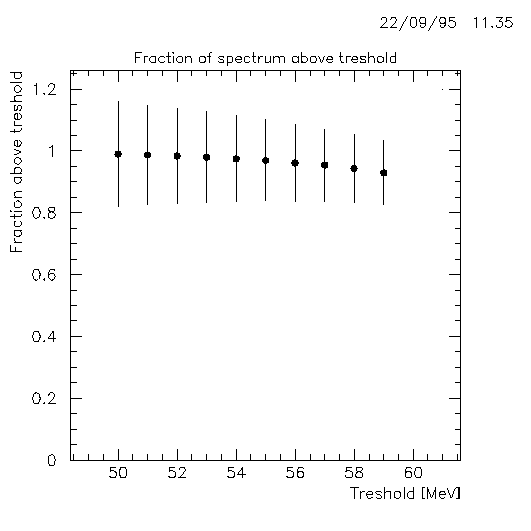
As final result of the response of the CsI array to 70 MeV gammas, a value of 6.7 MeV FWHM (Fig 15) is obtained. With the obtained parametrisation of the lineshape, one can calculate the fraction and its error of the spectrum which is above a given treshold. The result of this calculation is shown in figure 16.

Fig 16 PostScript

Ch. Broennimann, 19 Sept 1995