




5.4 Photoelectron Statistics
In a crystal which contains nearly all of the energy deposited by an incident
particle, the energy resolution is determined largely by the light output. The
intrinsic light output of CsI is about 4000 photons per MeV of energy deposit
[PDG 94]. The detected signal is quoted by the number of photoelectrons per MeV
(np) produced by the PMT. The relation between photons/MeV
produced and np involves factors like light collection
efficiency (depending on the geometry of the crystal) and quantum efficiency of
the PMT (15-20%). Values for np between 130 and 300
photoelectrons per MeV of large pure CsI-crystals were reported [Woo 90].
A determination of np can be based on the fact that the
photoelectron statistics follows a Poisson distribution, with
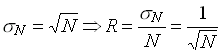 ,
(
5.6)
,
(
5.6)
where N is the mean value, s N the standard
deviation and R the associated resolution of the distribution. N
can be interpreted as the average number of photoelectrons produced by a
particle depositing the energy E,
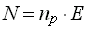 .
(
5.7)
.
(
5.7)
The measurement of the standard deviation s E for energy
distributions with varying mean energies E leads to a determination of the
number np:
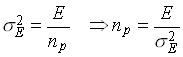 .
(
5.8)
.
(
5.8)
For every crystal the number np is measured with the
tomography apparatus (see. section 5.5). A light emitting diode (LED) is
connected to the open back face of each of the 6 crystals in the apparatus. The
LED's are pulsed with signals of various amplitudes (between 3 and 30V),
a fixed width of 20 ns and a frequency of 10Hz. The variation of the
amplitude from the LED driver (type LP100) is about 1%.
 Figure
5.6:
ADC spectrum of a HEXA crystal obtained from recording data with six different
intensities of the LED (top). Each peak is fitted with a gaussian, the
sigma2 of which is plotted against the associated mean value
(bottom). The parameter P2 of the linear fit is the inverse of the number of
photoelectrons per ADC channel (Eq. 5.8).
The amplitude of the LED pulses is varied and leads to a spectrum as shown in
Fig. 5.6 (top). One "LED-Run" includes data of LED pulses and simultaneously
data of cosmic muons penetrating the crystals. The data of cosmic muons are
needed for two reasons:
Figure
5.6:
ADC spectrum of a HEXA crystal obtained from recording data with six different
intensities of the LED (top). Each peak is fitted with a gaussian, the
sigma2 of which is plotted against the associated mean value
(bottom). The parameter P2 of the linear fit is the inverse of the number of
photoelectrons per ADC channel (Eq. 5.8).
The amplitude of the LED pulses is varied and leads to a spectrum as shown in
Fig. 5.6 (top). One "LED-Run" includes data of LED pulses and simultaneously
data of cosmic muons penetrating the crystals. The data of cosmic muons are
needed for two reasons:
1. The recorded cosmic ray spectrum for a crystal of a certain type is compared
to a simulation of cosmic rays penetrating a crystal of the same type which
leads to an absolute energy calibration.
2. A cosmic ray trigger in one of the six crystal produces an ADC pedestal
value for the remaining five crystal, which delivers the "zero energy" point.
A cosmic ray spectrum is shown in Fig. 5.7.
 Figure
5.7:
Cosmic ray spectrum from a "LED-run" of HEXA crystal. For a conversion of
ADC-channel to MeV scale the spectrum is compared to the result of a GEANT
simulation (Table 5.4).
The np-values obtained for the pibeta crystals (
Figure
5.7:
Cosmic ray spectrum from a "LED-run" of HEXA crystal. For a conversion of
ADC-channel to MeV scale the spectrum is compared to the result of a GEANT
simulation (Table 5.4).
The np-values obtained for the pibeta crystals (
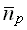 ~80)
are a factor of about two lower than expected. One reason seems to be the
partial coverage of the back face area of the crystals by using 3'' PMT's. The
back face of a pentagonal crystal is covered to 61%; for the hexagonal crystals
only about 40% is covered. A clear relation is observed between the area
covered by the PMT, i.e. the crystal type, and the measured number of
photoelectrons per MeV. A linear extrapolation to 1 (i.e. a total coverage of
the crystal back face by the PMT) leads to np~130.
~80)
are a factor of about two lower than expected. One reason seems to be the
partial coverage of the back face area of the crystals by using 3'' PMT's. The
back face of a pentagonal crystal is covered to 61%; for the hexagonal crystals
only about 40% is covered. A clear relation is observed between the area
covered by the PMT, i.e. the crystal type, and the measured number of
photoelectrons per MeV. A linear extrapolation to 1 (i.e. a total coverage of
the crystal back face by the PMT) leads to np~130.
Crystal
type
|
Cosmic
muon peak
|
PENT
|
39
MeV
|
HEXA
|
48
MeV
|
HEXB
|
50
MeV
|
HEXC
|
52
MeV
|
HEXD
|
51
MeV
|
Table
5.4:
Peak values of crystal spectra from a GEANT [Gea 94] simulation for cosmic
muons penetrating CsI-crystals.
According to equations 5.6 and 5.7 np~80 would lead to an
energy resolution of 1.3% (3.1% FWHM ). At 70 MeV this would correspond to
2.2 MeV (FWHM) which would be sufficient for the pion beta decay
experiment. It should be mentioned that not only the number of photoelectrons
per MeV contributes to the energy resolution of the crystals, but also the
effect of light collection non-uniformity must be added, when detecting
70 MeV photons or positrons.





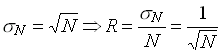 ,
(
5.6)
,
(
5.6)






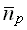 ~80)
are a factor of about two lower than expected. One reason seems to be the
partial coverage of the back face area of the crystals by using 3'' PMT's. The
back face of a pentagonal crystal is covered to 61%; for the hexagonal crystals
only about 40% is covered. A clear relation is observed between the area
covered by the PMT, i.e. the crystal type, and the measured number of
photoelectrons per MeV. A linear extrapolation to 1 (i.e. a total coverage of
the crystal back face by the PMT) leads to np~130.
~80)
are a factor of about two lower than expected. One reason seems to be the
partial coverage of the back face area of the crystals by using 3'' PMT's. The
back face of a pentagonal crystal is covered to 61%; for the hexagonal crystals
only about 40% is covered. A clear relation is observed between the area
covered by the PMT, i.e. the crystal type, and the measured number of
photoelectrons per MeV. A linear extrapolation to 1 (i.e. a total coverage of
the crystal back face by the PMT) leads to np~130.



