1. Introduction to the pb Experiment - 5.5 Light Collection Non-Uniformity

5.5 Light Collection Non-Uniformity

The light collection non-uniformity is strongly connected to the geometry of the detector. It can be determined by simultaneously recording tracks of particles penetrating the crystal and the resulting light output. This can be achieved by probing the crystal, positioned between MWPC's, with a particle beam or cosmic muons. From the MWPC-information a track through the crystal is reconstructed and the pathlength is calculated. For rectangular crystals the light over pathlength is constant along the crystal axis [Woo 90] but for the tapered pyramidal crystals the shape of the function depends on the actual geometry.

The optical properties of a crystal can be influenced by wrapping the side faces and covering the front face. Different wrapping materials were tested for maximal light output and minimal optical non-uniformity. Best results were obtained by wrapping the crystal with three layers of teflon-foil (total ~60µm thick) and one layer of aluminized Mylar (~20 µm) for optical insulation. Additional beam studies were performed to check the influence of the front face coverage on the light collection non-uniformity. Covering the crystal front-face with black paper turned out to be the optimal solution.

Figure 5.8: Six CsI-crystals as they are positioned in the tomography box. One of the chambers is mounted on the lid of the box, two chambers are below the box. The optical properties of each CsI-crystal are systematically studied in the tomography apparatus (Fig. 5.8) before the module is selected for the assembly into the calorimeter. Parameters like the attenuation length of CsI, the temperature dependence of the light output, and the F/T ratio for the wrapped crystal (see footnote on page 36) are determined. Of major importance is the determination of the non-uniformity caused by the generation and collection of the scintillation light.

Figure 5.9: The light non-uniformity obtained from the 2D-reconstruction procedure for one CsI-crystal of type HEXA. The vertical axis is the light output per unit pathlength. The horizontal axis are the mean values of the calculated entry (x₁, z₁) and exit point (x₂, z₂) of the muon at the surface of the crystal. The offset in the z-coordinate of about 29 cm is artificial. The PMT is located at (z₁ + z₂)/2 =52 cm. The tomography apparatus consists of a light-tight box enclosing the modules, three drift chambers for tracking of cosmic muons and two scintillator paddles below the bottom chamber used as triggers. The crystals are positioned in the box with an accuracy of about 1 mm. Each of the drift chambers has two orthogonal x, y-wire planes surrounded by three ground planes.

For a cosmic muon penetrating the apparatus, the hits in the 3 chambers allow a precise determination of the track. The segments of the cosmic ray paths in the CsI-crystals can be calculated and compared to the actual crystal signal. Only muons penetrating the crystals in almost vertical direction (polar angle q >85°) are accepted. This allows the determination of the light per unit pathlength along the crystal axis (axial, z-coordinate) and perpendicular (transversal, x-coordinate) to the crystal axis. The resulting light non-uniformity from this 2-dimensional reconstruction procedure for one CsI-crystal[13] is shown in Fig 5.9.

The cosmic ray tomography is a delicate project. It needs very careful tuning and calibration of the experimental apparatus as well as an elaborated analysis of the data. The quality of the data and their analysis are currently improved. The aim of the analysis is the quantification of the light non-uniformity for each crystal. Since the final data for each crystal was not available as the writing of this work was ongoing, only common features of the optical response as they are visible in Fig 5.9 can be given:

* bright spot at the front face (z = 0-5 cm) of the crystal.

* a "hole" in the response at z ~ 15-18 cm, where the light output is ~10-15% lower.

* bright zone at the back face in front of the PMT (z = 22 cm)

* dark zones at the edges of the crystal.

In order to incorporate the optical response in the simulation of the electromagnetic shower, it is parametrized by an analytic function f_lnu(r,z) which approximates the features listed above. The light non-uniformity function f_lnu(r,z) (Fig. 5.10) is calculated for each space point x, y, z in the body coordinate system of the volume of a crystal, with :

( 5.9)

The length of the crystal is l=22 cm, the "hole" in the response is assumed to be at z_d=15 cm. The parameter lnu corresponds to the difference between the light output at z=0 and z_d of the crystal. The parameters P_F and P_B account for the transverse non-uniformity at the front and back of the crystal, which is assumed to be parabolic. Best correspondence with the experimental data available was obtained with P_F=0.002, P_B=0.02 and lnu=0.12.

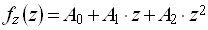Figure 5.10. Parametrization of the optical light non-uniformity for a HEXA type CsI-crystal by the function f_lnu(r,z), given in Eq. 5.9. The 3'' PMT is located at z=22 cm. The z-dependent function f_z in (5.9)

(5.10)

is constrained as follows:

f_z(z=0) = 1; f_z(z=z_d) = 0; f_z(z=l) =-1. (5.11)

The resulting parameters are:

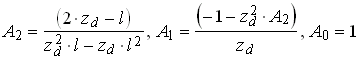. (5.12)

It should be mentioned that (5.9) represents a first approach to parametrize the optical non-uniformity of the crystal. The function f_lnu(r,z) is likely to change with the improved analysis of the tomography data. The aim of the tomography project is the parametrization of the optical response of each crystal in the pibeta calorimeter.

[13] The analysis of the data have been performed by E. Frlez (UVA).