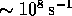The most precise measurement of the pion beta decay rate to date [McF-85] was carried with an in-flight decay technique. The decay in flight method measures the pion beta decay rate fairly directly by detecting a certain number of pions in a known amount of pion proper time. Moreover, although high pion beam intensity is required, the average raw rates in the detectors are lower by about two orders of magnitude than in the stopped pion experiment. However, important drawbacks to the in-flight technique limit possible improvements of the set-ups of previous experiments and dictate the choice of the experimental method for this precision measurement. The drawbacks to the in-flight technique are discussed below.
Firstly, the in-flight method requires an
absolute counting of beam pions as well as an absolute determination of the
detector acceptance, efficiency, and pion proper time in the decay region. No
scheme has been demonstrated to date to achieve an accuracy significantly
better than a percent in counting beam pions at intensities of
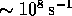and momenta greater than 400 MeV/c. A way around
the problem of absolute normalization, is to do a relative normalization using
a well measured decay channel of the pion. The only option is
.
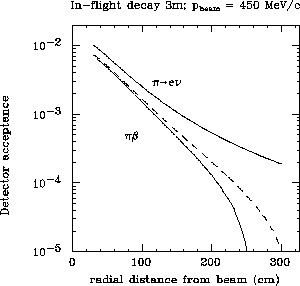
Figure: Radial dependence of
the in-flight detector acceptances for 
and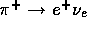 
assuming 3 m decay path and a beam
momentum of 450 MeV/c. The dashed line shows the change in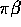 
acceptance corresponding to extending the detector inward radially by 5 cm at
the center.
However a precise knowledge of the
acceptances and conversion efficiencies for both decays is still required. As
shown in figure 
, the acceptances for both
decays differ by a factor of 2 for reasonable geometries so that the
uncertainties do not cancel out in the ratio.
Secondly, the absolute
determination of the effective acceptance of a 
detector at the desired
level of accuracy is difficult due to edge effects. The edge effects arise from
the opening to let the beam and the Michel positrons through. However, the edge
region contributes most significantly to the total acceptance as shown in
figure for a set-up with three meters decay region. A radial
uncertainty of 1 cm in 
fiducial area translates into a 
uncertainty in total acceptance.
Thirdly, the triggers: the pion decays occur over an extended
decay region. As a result, there is no unique correlation between the shower
and the coordinates of the conversion point. In a relative measurement,
an energy-angle cut is necessary for the identification of
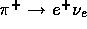events. The energy-angle cut requires the
placement of a tracking detector in front of the calorimeter. In a realistic
experimental situation, the tracking accuracy and thus the energy-angle cut
efficiency is limited by beam size, divergence and momentum distribution.
Moreover, the energy resolution in the calorimeter is important in isolating
the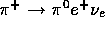 
and
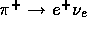decays from the background. In an in-flight
technique involving more energetic showers, it is more difficult to resolve the
separation of about 30 MeV.
Fourthly, rate limitations: due to the
high kinematic boost of all events, their energy separation in the detector is
difficult. Particularly troublesome are the radiative decays
and
. The effective
duty factor for in-flight measurement is 
, given the PSI beam
structure. This exacerbates the suppression of accidentally coincident
background events like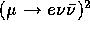 
. In order to suppress
them by a time-of-flight cut, a long beam line is needed, which reduces the
total available beam pions. Enlarging the shower detector does not work beyond
a certain point because the size of the opening determines the total acceptance
for pion beta events, not the outer boundary (see figure ).
Finally, size
and cost of the detector: figure gives a good indication of
the size requirements for an in-flight decay detector. For a calorimeter in
CsI like in the stopped experiment, the volume would be
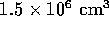and the cost about 
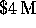. This is
more than four times the volume of a corresponding shower calorimeter in the
stopped experiment (see section 5.4).