



Next: Triggers
Up: Granularity of the
Previous: Calorimeter in Geant
The gamma rays and positrons of  --- this is approximately the
energy of the
--- this is approximately the
energy of the 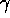 's from pion beta and
's from pion beta and 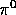 decays and
decays and 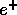 's from
's from
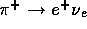 as explained in chapter 4 --- were thrown into the
apparatus according to the stopping distributions and tracked throughout the
detector volumes, keeping track of the location of the energy deposition at
each step.
as explained in chapter 4 --- were thrown into the
apparatus according to the stopping distributions and tracked throughout the
detector volumes, keeping track of the location of the energy deposition at
each step.

Figure: Profiles of the electromagnetic shower
spreading in the calorimeter. Shown here are the histograms of the means and FWHM's
of the energy deposited by the shower inside a conical fiducial subvolume of the
calorimeter. The conical subvolumes are defined by the half-opening angles,
 . Showers were initiated by
. Showers were initiated by 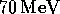 photons
(solid curves) and positrons (dashed curves) using the Geant simulation
package.
photons
(solid curves) and positrons (dashed curves) using the Geant simulation
package.
The energy deposited was then histogrammed into one degree conical
bins concentric with the direction of the original particle's momentum. From
figure  , it is concluded that:
, it is concluded that:
- The mean of the deposited energy as well as the full width half maximum
approach saturation within a cone of half-angle
 .
.
- The shower profiles initiated by
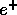 's are similar to that initiated
by
's are similar to that initiated
by 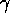 's particularly in the saturation region of the deposited energy:
this is important in controlling the systematic errors which result from the
normalization of pion beta events to
's particularly in the saturation region of the deposited energy:
this is important in controlling the systematic errors which result from the
normalization of pion beta events to 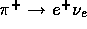 decays.
decays.
- As indicated by the arrow marked 1, if hit centrally, a detector module
will receive
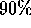 of the shower energy. At most three detector modules will
receive significant portions of the shower. As shown by the arrow marked 7,
clusters of 7 detectors constitute excellent trigger elements since
almost all of the shower energy is contained within the conical fiducial
volumes of seven modules. However, clusters of three are also
satisfactory.
of the shower energy. At most three detector modules will
receive significant portions of the shower. As shown by the arrow marked 7,
clusters of 7 detectors constitute excellent trigger elements since
almost all of the shower energy is contained within the conical fiducial
volumes of seven modules. However, clusters of three are also
satisfactory.
Therefore, the building blocks of the two main data triggers,  and
and
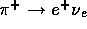 , are overlapping clusters of seven
crystals. To each cluster, there corresponds a symmetric one in the opposite
hemisphere. The determination of the clusters and their efficiency in
detecting the gamma rays and positrons (of
, are overlapping clusters of seven
crystals. To each cluster, there corresponds a symmetric one in the opposite
hemisphere. The determination of the clusters and their efficiency in
detecting the gamma rays and positrons (of 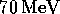 ) which indeed
deposit over
) which indeed
deposit over 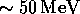 in the calorimeter, have been thoroughly
investigated. The threshold of
in the calorimeter, have been thoroughly
investigated. The threshold of 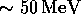 is selected so as to
discriminate against the Michel
is selected so as to
discriminate against the Michel 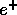 's whose spectrum extends up to
's whose spectrum extends up to
 as explained in chapter 4.
as explained in chapter 4. 
 's
and
's
and 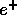 's were thrown into the apparatus and the energy deposited into each
cluster was recorded. A total of 100,000 shower histories were collected for
each type of particles. The vetoes, due to their role as shower vetoes, are
not included in the clustering scheme. In addition, a given module cannot
belong to more than three clusters: this avoids the degradation of the PMT
signals due to excessive splittings. The efficiency of the clustering
scheme in detecting the particles whose shower energies exceed the threshold
was defined as follows:
's were thrown into the apparatus and the energy deposited into each
cluster was recorded. A total of 100,000 shower histories were collected for
each type of particles. The vetoes, due to their role as shower vetoes, are
not included in the clustering scheme. In addition, a given module cannot
belong to more than three clusters: this avoids the degradation of the PMT
signals due to excessive splittings. The efficiency of the clustering
scheme in detecting the particles whose shower energies exceed the threshold
was defined as follows:




Next: Triggers
Up: Granularity of the
Previous: Calorimeter in Geant
Bernward Krause
Mon Jan 15 14:57:06 MET 1996
 --- this is approximately the
energy of the
--- this is approximately the
energy of the 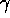 's from pion beta and
's from pion beta and 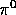 decays and
decays and 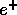 's from
's from
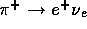 as explained in chapter 4 --- were thrown into the
apparatus according to the stopping distributions and tracked throughout the
detector volumes, keeping track of the location of the energy deposition at
each step.
as explained in chapter 4 --- were thrown into the
apparatus according to the stopping distributions and tracked throughout the
detector volumes, keeping track of the location of the energy deposition at
each step.





 . Showers were initiated by
. Showers were initiated by 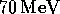 photons
(solid curves) and positrons (dashed curves) using the Geant simulation
package.
photons
(solid curves) and positrons (dashed curves) using the Geant simulation
package.
 .
.
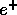 's are similar to that initiated
by
's are similar to that initiated
by 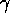 's particularly in the saturation region of the deposited energy:
this is important in controlling the systematic errors which result from the
normalization of pion beta events to
's particularly in the saturation region of the deposited energy:
this is important in controlling the systematic errors which result from the
normalization of pion beta events to 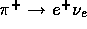 decays.
decays.
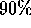 of the shower energy. At most three detector modules will
receive significant portions of the shower. As shown by the arrow marked 7,
clusters of 7 detectors constitute excellent trigger elements since
almost all of the shower energy is contained within the conical fiducial
volumes of seven modules. However, clusters of three are also
satisfactory.
of the shower energy. At most three detector modules will
receive significant portions of the shower. As shown by the arrow marked 7,
clusters of 7 detectors constitute excellent trigger elements since
almost all of the shower energy is contained within the conical fiducial
volumes of seven modules. However, clusters of three are also
satisfactory.
 and
and
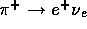 , are overlapping clusters of seven
crystals. To each cluster, there corresponds a symmetric one in the opposite
hemisphere. The determination of the clusters and their efficiency in
detecting the gamma rays and positrons (of
, are overlapping clusters of seven
crystals. To each cluster, there corresponds a symmetric one in the opposite
hemisphere. The determination of the clusters and their efficiency in
detecting the gamma rays and positrons (of 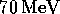 ) which indeed
deposit over
) which indeed
deposit over 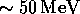 in the calorimeter, have been thoroughly
investigated. The threshold of
in the calorimeter, have been thoroughly
investigated. The threshold of 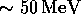 is selected so as to
discriminate against the Michel
is selected so as to
discriminate against the Michel 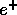 's whose spectrum extends up to
's whose spectrum extends up to
 as explained in chapter 4.
as explained in chapter 4. 
 's
and
's
and 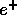 's were thrown into the apparatus and the energy deposited into each
cluster was recorded. A total of 100,000 shower histories were collected for
each type of particles. The vetoes, due to their role as shower vetoes, are
not included in the clustering scheme. In addition, a given module cannot
belong to more than three clusters: this avoids the degradation of the PMT
signals due to excessive splittings. The efficiency of the clustering
scheme in detecting the particles whose shower energies exceed the threshold
was defined as follows:
's were thrown into the apparatus and the energy deposited into each
cluster was recorded. A total of 100,000 shower histories were collected for
each type of particles. The vetoes, due to their role as shower vetoes, are
not included in the clustering scheme. In addition, a given module cannot
belong to more than three clusters: this avoids the degradation of the PMT
signals due to excessive splittings. The efficiency of the clustering
scheme in detecting the particles whose shower energies exceed the threshold
was defined as follows:
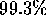 and
and  efficient for
70 MeV photons and positrons respectively. This suggests that, with the present
cluster configuration, about seven out of one thousand pion beta decay events will
not be detected although these events will deposit more than the threshold energy
in the calorimeter.
efficient for
70 MeV photons and positrons respectively. This suggests that, with the present
cluster configuration, about seven out of one thousand pion beta decay events will
not be detected although these events will deposit more than the threshold energy
in the calorimeter.

 .
. at
50 MeV. A small fraction (
at
50 MeV. A small fraction ( ) of Michel events will deposit more than 50 MeV
in the calorimeter and fire at least one cluster. The performance of the clustering
method as a function of trigger threshold is displayed in figure
) of Michel events will deposit more than 50 MeV
in the calorimeter and fire at least one cluster. The performance of the clustering
method as a function of trigger threshold is displayed in figure