 in electromagnetic interactions (EM) can
be written as:
in electromagnetic interactions (EM) can
be written as:




The Lagrangian density  in electromagnetic interactions (EM) can
be written as:
in electromagnetic interactions (EM) can
be written as:
where 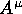 is the 4-vector potential. The interpretation of
is the 4-vector potential. The interpretation of
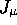 as current follows from the fact that
as current follows from the fact that 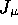 satisfies
the current conservation requirement. For illustration, consider an
electron-proton scattering. In one photon-exchange approximation, the
scattering amplitude is:
satisfies
the current conservation requirement. For illustration, consider an
electron-proton scattering. In one photon-exchange approximation, the
scattering amplitude is:
where the electron current takes the form:
and the proton current is written as:
 is the fine structure constant; k,
is the fine structure constant; k,  are the initial
and final 4-momenta of the electron; p,
are the initial
and final 4-momenta of the electron; p,
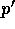 the corresponding 4-momenta of the proton and q is the momentum
transferred:
the corresponding 4-momenta of the proton and q is the momentum
transferred:
 is constructed from the proton 4-momenta and the
is constructed from the proton 4-momenta and the
 matrices. Due to Lorentz invariance and parity conservation
of EM interactions
matrices. Due to Lorentz invariance and parity conservation
of EM interactions 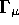 can only be vectors. Therefore, the hadronic
current is:
can only be vectors. Therefore, the hadronic
current is:
The quantities  are functions of
are functions of  only because
only because  can be
expressed as a function of
can be
expressed as a function of  and the masses involved. Using the following
identities
and the masses involved. Using the following
identities
and
the terms involving 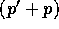 can be incorporated into other factors and
can be incorporated into other factors and
 reduces to the following:
reduces to the following:
where  is constant and M is the proton mass. The factor
is constant and M is the proton mass. The factor
 is inserted to make
is inserted to make 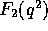 coincide with the conventional
definition of the EM form factor. The current
conservation requirement leads to
coincide with the conventional
definition of the EM form factor. The current
conservation requirement leads to 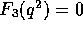 for elastic scattering (
for elastic scattering (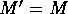 ).
The electric and magnetic form factors
).
The electric and magnetic form factors  and
and  can be
shown to be linear combinations of
can be
shown to be linear combinations of  and
and 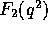 . In
the non-relativistic limit,
. In
the non-relativistic limit,  and
and 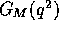 are
interpreted as the
Fourier transforms of the charge and the magnetic moment distributions
inside the nucleus.
are
interpreted as the
Fourier transforms of the charge and the magnetic moment distributions
inside the nucleus.