



Next: Cabibbo Universality
Up: Conserved Vector Current
Previous: Electromagnetic Current
The examination of the EM interactions (equation ( )) and weak
interactions (equation (
)) and weak
interactions (equation ( )) suggests that G essentially replaces
)) suggests that G essentially replaces
 . Therefore G has the dimension of
. Therefore G has the dimension of 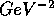 while
while  is dimensionless. By analogy to EM interactions which are
mediated by photons, weak interactions are assumed to be mediated by vector
bosons. In contrast to the photon, these vector bosons must be massive
otherwise they would be directly produced in weak decays. Needless to say,
the existence of these vector bosons and their masses have been confirmed
experimentally. The decay amplitude is of the form:
is dimensionless. By analogy to EM interactions which are
mediated by photons, weak interactions are assumed to be mediated by vector
bosons. In contrast to the photon, these vector bosons must be massive
otherwise they would be directly produced in weak decays. Needless to say,
the existence of these vector bosons and their masses have been confirmed
experimentally. The decay amplitude is of the form:

where 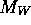 and q are the mass and the momentum carried by the vector boson
mediating the interaction; g is the dimensionless weak coupling constant and
the factor
and q are the mass and the momentum carried by the vector boson
mediating the interaction; g is the dimensionless weak coupling constant and
the factor 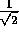 is inserted for the conventional definition of
g. In the situations where
is inserted for the conventional definition of
g. In the situations where 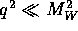 (
( -decay and
-decay and
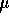 -decay
for instance) the interaction is essentially at a point. By comparing
equation (
-decay
for instance) the interaction is essentially at a point. By comparing
equation ( ) to (
) to ( ) one has:
) one has:

For illustration, consider the neutron- decay:
decay:

The decay amplitude is:

where 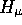 and
and 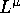 are the hadronic and the
leptonic weak current:
are the hadronic and the
leptonic weak current:
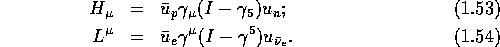
The hadronic current can be rewritten as:
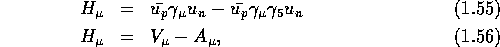
where  and
and 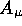 are the weak hadronic vector and
axial-vector currents respectively. Following the arguments used in
the EM case,
are the weak hadronic vector and
axial-vector currents respectively. Following the arguments used in
the EM case, 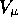 becomes:
becomes:
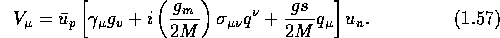
The similarity between 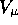 and the EM current
(equation (
and the EM current
(equation ( )) should be apparent. In EM, the charge is
strictly conserved even for strong interacting particles. Furthermore,
EM interactions are vector type of interactions with the coupling
constant directly related to the charge:
)) should be apparent. In EM, the charge is
strictly conserved even for strong interacting particles. Furthermore,
EM interactions are vector type of interactions with the coupling
constant directly related to the charge:

The weak vector current is assumed to be conserved with a universal
coupling constant in an analogy to the EM vector current. This
assumption is the CVC hypothesis. The form factor 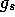 in
equation (
in
equation ( ) vanishes as a result.
) vanishes as a result.
The CVC hypothesis can also be formulated using isospin formalism as
follows: one defines a spinor
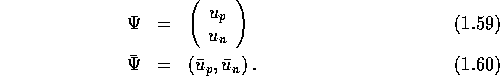
Using the Pauli matrices

the EM current 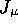 and the weak vector current
and the weak vector current  are
written as:
are
written as:
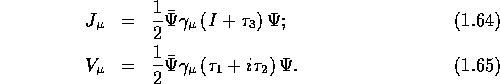
The EM current consists of the isoscalar part
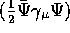 which satisfies the current
conservation requirement:
which satisfies the current
conservation requirement:
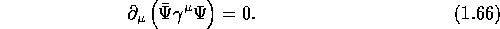
The isovector currents are as follows:
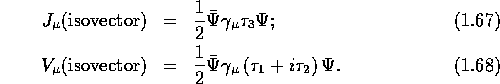
The CVC hypothesis assumes that these isovector currents are only
different components of the same isospin current

 is not conserved by
itself unless a pionic contribution is added to it; in the case of
neutron decay for instance, only a fraction of its lifetime neutron
exists as a bare neutron; for the rest of its lifetime, the neutron is
a proton surrounded by a "pion cloud". Like
is not conserved by
itself unless a pionic contribution is added to it; in the case of
neutron decay for instance, only a fraction of its lifetime neutron
exists as a bare neutron; for the rest of its lifetime, the neutron is
a proton surrounded by a "pion cloud". Like
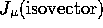 ,
,  needs to be
supplemented with a pionic term to satisfy current conservation.
needs to be
supplemented with a pionic term to satisfy current conservation.
In conclusion, the assumption that the isovector currents
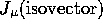 and
and  are
different components of the same current amounts to attributing the
same interaction strength to the pion-lepton vertices as to the baryon-lepton
vertices. Furthermore, since strong interactions are charge independent (to a
good approximation), one is led to the conservation of isospin --- pionic plus
baryonic --- which is a generalization of conservation of charge.
are
different components of the same current amounts to attributing the
same interaction strength to the pion-lepton vertices as to the baryon-lepton
vertices. Furthermore, since strong interactions are charge independent (to a
good approximation), one is led to the conservation of isospin --- pionic plus
baryonic --- which is a generalization of conservation of charge.




Next: Cabibbo Universality
Up: Conserved Vector Current
Previous: Electromagnetic Current
Bernward Krause
Mon Jan 15 14:57:06 MET 1996
 )) and weak
interactions (equation (
)) and weak
interactions (equation ( )) suggests that G essentially replaces
)) suggests that G essentially replaces
 . Therefore G has the dimension of
. Therefore G has the dimension of 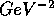 while
while  is dimensionless. By analogy to EM interactions which are
mediated by photons, weak interactions are assumed to be mediated by vector
bosons. In contrast to the photon, these vector bosons must be massive
otherwise they would be directly produced in weak decays. Needless to say,
the existence of these vector bosons and their masses have been confirmed
experimentally. The decay amplitude is of the form:
is dimensionless. By analogy to EM interactions which are
mediated by photons, weak interactions are assumed to be mediated by vector
bosons. In contrast to the photon, these vector bosons must be massive
otherwise they would be directly produced in weak decays. Needless to say,
the existence of these vector bosons and their masses have been confirmed
experimentally. The decay amplitude is of the form:





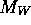 and q are the mass and the momentum carried by the vector boson
mediating the interaction; g is the dimensionless weak coupling constant and
the factor
and q are the mass and the momentum carried by the vector boson
mediating the interaction; g is the dimensionless weak coupling constant and
the factor 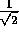 is inserted for the conventional definition of
g. In the situations where
is inserted for the conventional definition of
g. In the situations where 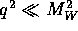 (
( -decay and
-decay and
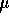 -decay
for instance) the interaction is essentially at a point. By comparing
equation (
-decay
for instance) the interaction is essentially at a point. By comparing
equation (
 decay:
decay:


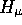 and
and 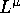 are the hadronic and the
leptonic weak current:
are the hadronic and the
leptonic weak current:
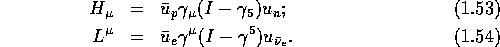
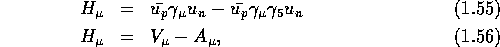
 and
and 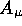 are the weak hadronic vector and
axial-vector currents respectively. Following the arguments used in
the EM case,
are the weak hadronic vector and
axial-vector currents respectively. Following the arguments used in
the EM case, 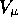 becomes:
becomes:
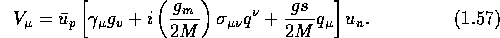
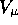 and the EM current
(equation (
and the EM current
(equation (
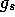 in
equation (
in
equation (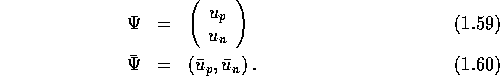

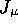 and the weak vector current
and the weak vector current  are
written as:
are
written as:
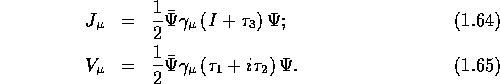
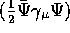 which satisfies the current
conservation requirement:
which satisfies the current
conservation requirement:
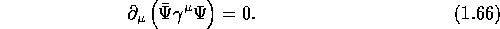
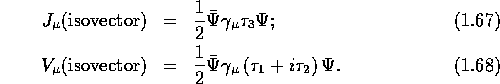

 is not conserved by
itself unless a pionic contribution is added to it; in the case of
neutron decay for instance, only a fraction of its lifetime neutron
exists as a bare neutron; for the rest of its lifetime, the neutron is
a proton surrounded by a "pion cloud". Like
is not conserved by
itself unless a pionic contribution is added to it; in the case of
neutron decay for instance, only a fraction of its lifetime neutron
exists as a bare neutron; for the rest of its lifetime, the neutron is
a proton surrounded by a "pion cloud". Like
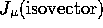 ,
,  needs to be
supplemented with a pionic term to satisfy current conservation.
needs to be
supplemented with a pionic term to satisfy current conservation.
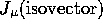 and
and  are
different components of the same current amounts to attributing the
same interaction strength to the pion-lepton vertices as to the baryon-lepton
vertices. Furthermore, since strong interactions are charge independent (to a
good approximation), one is led to the conservation of isospin --- pionic plus
baryonic --- which is a generalization of conservation of charge.
are
different components of the same current amounts to attributing the
same interaction strength to the pion-lepton vertices as to the baryon-lepton
vertices. Furthermore, since strong interactions are charge independent (to a
good approximation), one is led to the conservation of isospin --- pionic plus
baryonic --- which is a generalization of conservation of charge.