




Leptons participate in the weak interactions via the left-handed doublets:

Suppose  and
and 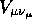 are the relative sizes
of the
are the relative sizes
of the
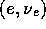 and
and  couplings. EM interactions
do not
distinguish e from
couplings. EM interactions
do not
distinguish e from  . Similarly, in weak interactions,
. Similarly, in weak interactions,
 [Got-84]. By redefining the weak
coupling constant,
[Got-84]. By redefining the weak
coupling constant,  . This is the
symmetry of the weak interaction under the exchange
. This is the
symmetry of the weak interaction under the exchange
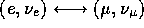 . Because the neutrinos
are massless,
. Because the neutrinos
are massless,
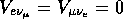 . The inclusion of
the third doublet of left-handed leptons
. The inclusion of
the third doublet of left-handed leptons

leads to:

In the quark sector, one has the left-handed fermion states
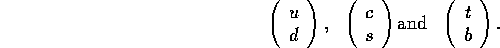
It is not quite correct to extend the lepton universality to the
quarks. That will lead to transitions between
 ,
,  and
and
 only. However, decays such as
only. However, decays such as
 occur. Since
occur. Since  is made up of
u and
is made up of
u and 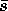 quarks, there must be a weak current which couples
u and
quarks, there must be a weak current which couples
u and  , that is
, that is 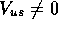 . In order to avoid the
introduction of a new coupling constant for quarks --- preserve
universality --- Cabibbo assumed that the weak interaction rotates quark
states. Subsequently, Kobayashi and Maskawa generalized Cabibbo's work to
three generations:
. In order to avoid the
introduction of a new coupling constant for quarks --- preserve
universality --- Cabibbo assumed that the weak interaction rotates quark
states. Subsequently, Kobayashi and Maskawa generalized Cabibbo's work to
three generations:

In other word, the quark states u, 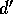 , c,
, c,  , t,
, t,  are
eigenstates of the weak interaction while the states u, d, c, s,
t, b are the mass eigenstates of the flavor-preserving strong
interaction. The weakly charged current
are
eigenstates of the weak interaction while the states u, d, c, s,
t, b are the mass eigenstates of the flavor-preserving strong
interaction. The weakly charged current  of the quarks is:
of the quarks is:
where U is a  matrix known as the
Cabibbo-Kobayashi-Maskawa (CKM) mixing matrix:
matrix known as the
Cabibbo-Kobayashi-Maskawa (CKM) mixing matrix:
or
where  ,
, 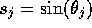 ;
; 
 are the Cabibbo angles and
are the Cabibbo angles and  is a phase factor. At four-quark
is a phase factor. At four-quark
 level U reduces to a real
level U reduces to a real  matrix
and the theory can be shown to be CP invariant. However, with the
extension to t and b quarks, the mixing matrix contains a phase
factor and for that reason the theory violates
matrix
and the theory can be shown to be CP invariant. However, with the
extension to t and b quarks, the mixing matrix contains a phase
factor and for that reason the theory violates  [Hal-84].
[Hal-84].
The implication is that for nuclear beta decays involving
only vector interactions, one must replace the coupling
constant G of equation ( ) by
) by
In the case of a pure leptonic decay ( -decay
for instance), there is no mixing:
-decay
for instance), there is no mixing:
The top row the CKM matrix (equations  and
and  ) provides the
unitarity test
) provides the
unitarity test
which must be satisfied if the Standard Model with three generations is
correct.



