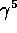 is referred to as the chirality operator which
transforms as:
is referred to as the chirality operator which
transforms as:




The operator 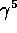 is referred to as the chirality operator which
transforms as:
is referred to as the chirality operator which
transforms as:

With the momentum 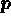 along the z-axis, the helicity operator
becomes:
along the z-axis, the helicity operator
becomes:
Since
we have:
It follows that the solutions to the Dirac equation for a
massless fermion are eigenstates of 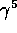 . This is not the case
for a massive fermion. However, the wavefunction can be written as a
linear combination of the right-handed and left-handed components:
. This is not the case
for a massive fermion. However, the wavefunction can be written as a
linear combination of the right-handed and left-handed components:
where
Consider a 4-fermion interaction 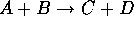 which is assumed
to be invariant under the chiral transformation defined above. The
interaction amplitude can be written as:
which is assumed
to be invariant under the chiral transformation defined above. The
interaction amplitude can be written as:
Chiral invariance leads to:
In order for the amplitude  to be invariant under a Lorentz
transformation, the operator O can be shown to be a linear
combination of the following:
to be invariant under a Lorentz
transformation, the operator O can be shown to be a linear
combination of the following:

where
It follows that:
and
Of these five possible operators, only the vector and
axial-vector operators V and A anticommute with 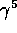 . Therefore,
. Therefore,
From equation ( ), one has a=-b since
), one has a=-b since
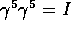 and
and  anticommutes with
anticommutes with
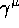 . The operator O becomes:
. The operator O becomes:
where a is a constant. The amplitude M takes the form:
where the currents 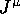 and
and  are given below:
are given below:
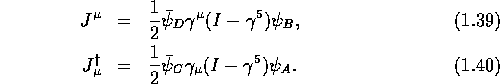
This is the modification of the current-current Fermi interaction --- at a point --- to accommodate the axial-vector contribution originally absent in Fermi's theory.
It should be pointed out that theoretically, one could arrive at a form of the weak charged current in which only S, T and P contribute. However, the experimental evidences are in favor of the (V,A) form.
The following conclusions follow from the V-A form
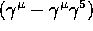 of the weakly charged
current [Che-79]:
of the weakly charged
current [Che-79]:
 leads to a neutrino with positive helicity which is not allowed.
leads to a neutrino with positive helicity which is not allowed.
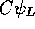 (where
(where 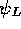 describes the neutrino) leads
to an antineutrino still with negative helicity: this is not allowed.
describes the neutrino) leads
to an antineutrino still with negative helicity: this is not allowed.
 is conserved. Since T reverses both spin and
momentum, the original state is unchanged.
is conserved. Since T reverses both spin and
momentum, the original state is unchanged.
Naturally, one would hope that all weak processes are described the
V-A interactions with a universal coupling constant.



