The Dirac equation for a massive fermion of momentum 
is:
However, the free particle must satisfy the energy-momentum requirement
which allows the determination of the coefficients 
and
:
and
where 
are the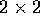 
Pauli matrices and
I is the 
unit matrix. In covariant form,
equation (
) can be written as:
where
With
where
equation () leads, after some manipulation, to the following:
In the case of a massless fermion, a neutrino for instance, the above relations are decoupled:
Each of these equations is based on the relativistic energy-momentum
relation 
and therefore has one positive
and one negative solutions. For 
,
and
where 
is the
helicity operator. 
describes a left-handed neutrino (negative
helicity) whereas 
describes a right-handed (positive helicity) antineutrino.
The other solution with 
satisfies
and
In this case,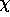 
and 
describe a right-handed antineutrino and a left-handed
neutrino, respectively.
Consider the case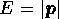 
and the operator
where
The action of the operator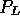 
on the the spinor u gives:
Similarly,
So, the operator 
projects out the left-handed spinor 
whereas
projects out the right-handed spinor 
.
