In the 1997 data run, there were two beams: one of 70 MeV/c positrons, and
one of 116 MeV negative pions (see Chapter 2). Clearly, the 70 MeV/c
positrons can be treated
as monoenergetic particles in the gain matching. Likewise, the 116 MeV/c 
beam incident on the liquid hydrogen target leads to the reaction
, where the outgoing photon is monoenergetic at 129 MeV/c.
Consequently, it is possible to apply nearly identical gain matching algorithms
to data from both beams, based on the presence of monoenergetic particles
in each one.
The detector gain matching for monoenergetic particles is accomplished by an iterative algorithm which aligns the peak positions of the summed 44 CsI and 64 NaI detector histograms. Each of these histograms contains the summed energy deposited into the calorimeter per event, with the requirement that 50% of the shower be contained in the crystal of interest. By applying the software gain corrections produced in the gain matching algorithm, the peak positions are placed into a channel which is close to the individual online peak positions. These online peak positions were chosen based on the following:
2-3%) PMT high voltages, the
129 MeV photon peak is placed into channel 3000.
Finally, after the gain matching, an absolute energy calibration is performed
based on the results of the GEANT [7] Monte Carlo simulation of
the experiment.
The first step in the gain matching algorithm is to determine which crystals were actually illuminated by the monoenergetic particles. This is done simply by counting the number of events per detector in the histograms described in the previous paragraph. Only crystals which contain a minimum number of events in the histogram are included in the algorithm.
Next, the peak
positions of the summed spectra are determined through a fit with a
Gaussian-exponential function. This function f(x) is described
by four parameters: height of the Gaussian h, mean of the Gaussian 
,
standard deviation of the Gaussian 
, and a transition point t
between the Gaussian and exponential function (see Fig. 4.5).
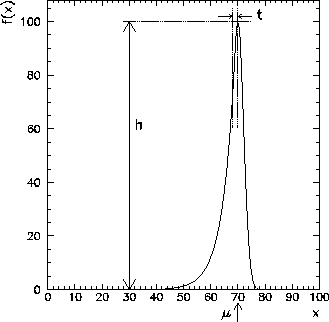
Figure 4.5: Gaussian-exponential function f(x), defined by the height h of the Gaussian,
the mean of the Gaussian, the standard deviation of the Gaussian, and
the transition point t between Gaussian and exponential.
By requiring that f(x) and 
be continuous at 
, the function
takes the following form:
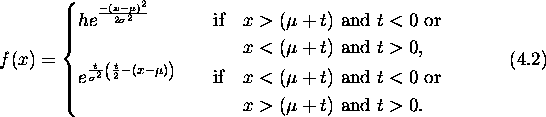
A typical fit with this function to a data spectrum resulting from a 70 MeV
monoenergetic positron beam is shown in Fig. 4.6.
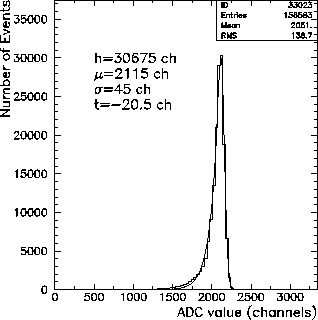
Figure 4.6: Fit with a Gaussian exponential function, to data resulting from a
70 MeV monoenergetic positron beam.
After determining the peak position from the fit to the data, the gain correction
factor Y is calculated as
where X is the required peak position. The new gain 
is related to the
previously calculated gain G by
The uncertainty in is propagated through the iterations.
From the theory of error propagation [2], for x= f(u,v),
and the error in the correction factor Y is calculated to be
Hence, the uncertainty in is propagated through iterations of the
algorithm as
The gain matching algorithm is allowed to iterate until the average change in
the gains 
is less than the average standard deviation of the correction factors Y,
When this condition is met, the gain matching algorithm has converged.
Fig. 4.7 shows a plot of the standard deviation of the
CsI calorimeter's response function in a 70 MeV positron beam plotted against the
iteration number of the gain matching algorithm. One can see that the energy
resolution of the calorimeter improves with the convergence of the algorithm.
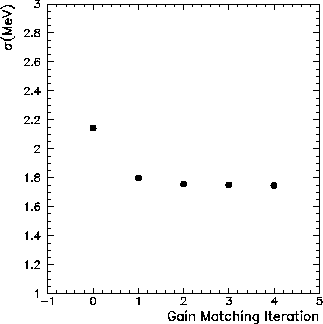
Figure 4.7: Standard deviation of the CsI response function in a
70 MeV positron beam, plotted against the iteration number of the gain
matching algorithm.