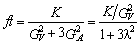transitions.
After a remeasurement of four half-lives Koslowski et al. [Kos97] are obtaining
an average f't-value of (3072.3 ± 2.0) s which results[7] in Vud = 0.9740±0.0005.
Although they claim no significant deviation from CVC predictions at the
4*10-4 level, the unitarity test fails by more than two standard
deviations since V1 = = 0.9972 ± 0.0013. Opposed to that
finding Wilkinson [Wil94] propagates a Z2-dependent radiative
correction based on theoretical considerations [Sir87] which can be achieved
using a three parameter fit of the 9 precision data of superallowed
transitions. He obtains V1=1.0000±0.0017 which is also
supported by the least c 2-value for that three parameter fit;
but the implementation of a Zn-dependent correction due to a
phenomenologically QCD-dependence is not necessarily consistent with the CVC
hypothesis anymore. Although Wilkinson can add the datum of the 10C
superallowed b -decay on cost of the a slightly higher error
[Wil94], Savard et al.[Sav95] favour a linear extrapolation to f't(Z=0)
because of a significantly lower systematical error. Their result shows
consistency with the one of [Kos97] at a slightly higher uncertainty.
Neutron lifetime measurements - and hence the evaluation of neutron
ft-values - are of similar precision as superallowed nuclear
b -decay transition measurements; but due to the influence of the
strong interaction the axialvector coupling constant GA must be
obtained independently to calculate V1. The ft-value of the
free neutron decay is related to the coupling constants as follows
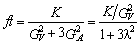.While GA can not be measured directly, [lambda] is available through the angular distribution of the electrons with respect to the direction of the decaying polarised neutron. The so-called beta decay asymmetry parameter A0 was obtained to -0.1160±0.0015 [Lia97] and is related to [lambda] by
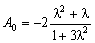and hence [lambda] = -1.266±0.004. Measurements of the neutron lifetime [tau]n have been achieved using two methods; either using neutrons from a reactor or an accelerator or via storage of (ultra-)cold neutrons (UCN). Unfortunately the obtained results differs significantly (more than two standard deviations) from each other.
The method of neutron storage allows the determination of [tau]n by the decay law
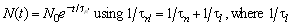
represents the probability for neutron losses at the side walls of the trap. An average of the so obtained results gives [tau]n=885.9s±1.7s [Mos96]. With beam methods [tau]n is determined by measuring the change in the beam flux due to neutron b -decay. The neutron lifetime then is proportional to the ratio of neutron amount N divided by the amount of neutron decays (dN/dt). The latter is obtained using the proton or electron energy spectrum. The obtained neutron lifetime from beam experiments amounts in average to [tau]n=894.2s±4.2s [Mos96].
Although the averaged value of 886.7±1.9 [PDG98] - in connection with the above given [lambda] - is consistent with the unitarity of the CKM-matrix (V1=1.0005±0.0032), the inherent inconsistency of neutron lifetime measurements and the obtained asymmetry parameter value demands an independent test. Nevertheless, more accurate measurements are planned for both beam neutron decay [Mak98] and stored UCN [Sch95,Uts98].
Previous measurements of the pion beta decay rate are in good agreement with the standard model but have too large an uncertainty to prove theoretical calculations. The most recent determinations of the pion beta decay rate are:
Depommier et al. (1968): 0.38±0.03 s-1 [Dep68]
McFarlane et al. (1985): 0.394±0.015 s-1 [McF85]
These experiments that measured the pion beta decay rate prior to PiBeta are
suffering a high uncertainty. In addition to a relatively low total number of
p b events, the major contribution to the error origins from the
determination of the detector efficiency or acceptance.
Depommier et al. [DEP68] used a carbon degrader and an active CH2
target to stop 77 MeV pions at a rate of ~3.5*104/s. Their
calorimeter consisted of an array of eight lead-glass counters that covered 60%
of the 4 p sr solid angle. The radial thickness was equivalent to 6.8
radiation lengths. The detector efficiency was calibrated using the charge
exchange reaction p -p-> p 0n (SCX) followed by
p 0-> g g with a precision of 3.6%. This way they
obtained a branching ratio of
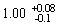*10-8.
Seventeen years later McFarlane et al. [McF85] used an intense pion beam
(2*108 p /s) at LAMPF to measure the branching ratio with higher
precision. The measurement of the decay in flight helped to reduce the
background due to the Michel decay of the muon at the cost of a low acceptance
for the detection of a photon pair (and thus a p b event). For the
calibration they inserted either a liquid hydrogen target or a
CH2-target close to the p -decay region. Thus they obtained energy
scale, conversion efficiency and absolute timing of their apparatus by
detecting monoenergetic p 0s from either SCX or p +C
-> p 0+X ( p -C -> p 0+X',
respectively). Together with the total number of pions which was determined
using the averaged counting rate of three monitors they obtained a branching
ratio BR p b of 1.026±0.039*10-8.
Subsequently, a remeasurement of the pion beta decay with highest precision
requires both an intense pion beam and a high detection efficiency. Both can be
achieved with the PiBeta detector at PSI. To overcome the problem of the
precise determination of the detector efficiency and of the exact pion stop
rate a relative measurement was considered. Since the branching ratio of the
p +->e+ n e decay is known to a
precision of 0.3% [Cza93] it is an excellent source for a normalization.
For not being restricted by the finite detector size (which would mean low
efficiency) a stopped pion experiment is advisable; but due to the main pion
decay (see Table 2-3) this results in a large positron background via the
p ->µ->e decay chain. The Michel positron background can be well
separated with a good energy resolution of the calorimeter since the positron
of the decay p +->e+ n e has an energy
of 69.78 MeV while the so-called Michel-decay
µ+->e+ n eµ
results in 52.83 MeV positrons at most. (The muon from
p +->µ+ n µ cannot leave the
target and decays at rest.) Michel positrons can be further suppressed by the
long muon decay time of 2.2 µs, compared to the pion life time of 26 ns.
Furthermore additional background from hadronic reaction of the pions with
matter (mostly SCX) must be suppressed. This is a) possible through the time
structure (hadronic events are prompt) and b) with a plastic scintillator
hodoscope.
[8] A previous result [lambda]=-1.254±0.004 [Ero90] differs significantly