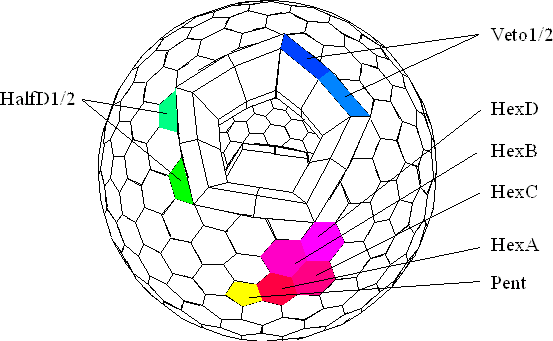







Figure 3-2 One of 60 basic triangles forming the calorimeter sphere. It is showing a fifth of the PENT, two halves of the HEX B and furthermore a HD1 plus a HD2 would form a HEX D.
The calorimeter must provide good energy and angular resolution as well as high stopping power for both ~70 MeV photons and positrons. Furthermore a fast response and reasonable costs are required. This was achieved by using 240 pure CsI crystals with a length of 22 cm corresponding to 12 radiation lengths. They are forming a partial sphere that covers 77% of the full 4 p sr solid angle. The calorimeter was designed using a class II geodesic breakdown of an icosahedron [Ass95].
Thus, the sphere is approximated by 60 triangles (or 12 pentagons, respectively) which leads to a repeating structure at f n=36°+(n-1)*72° for one hemisphere and 180°- f n for the other (compare with Figure 2-6). At the poles two pentagons were omitted for beam entrance and readout access. Instead, ten flat crystals on either side act as a veto for shower losses and beam particles. The remaining ten pentagons (plus overlapping crystals) act as superclusters for the trigger that is sensitive to two photons in opposite arrays of the sphere.
In order to reach high granularity - and hence provide a good angular resolution - each of these basic triangles consists of 4 1/5 crystals. Due to the curvature of these basic triangles we end up with 4 types of full and two of half hexagonal truncated pyramids, one pentagonal pyramid and two different veto crystals.





