





3.1 Properties of CsI
Asking for a fast and dense scintillating material with relatively high light
yield, pure CsI was the only choice. It shows two main emission components. One
in the near UV region at 310 nm and one at 460nm (the properties of CsI are
summarized in Table 3-1). In comparison to BaF2, CsI provides a
better suited wavelength for PMT readout and a shorter radiation length. BGO is
not suitable because of its long decay time of ~240 ns. Such a slow calorimeter
response would lead to multiple coincidences and reduced energy resolution due
to pile up, since i) the pion decay time is faster by an order of magnitude and
ii) the time structure of the accelerator is 19.75 ns.
Density
|
4.51
g /cm3
|
Radiation
length X0
|
1.85
cm
|
Molière
radius RM
|
3.8
cm
|
Atomic
Number Z
|
55,
53
|
Peak
wavelength
|
310
nm / 460 nm
|
Refractive
Index (@ 310 nm)
|
1.95
|
Decay
time (fast/slow)
|
~15
ns / ~ 1 µs
|
Lightyield
(fast component)
|
~
100 Photoel./MeV
|
Temperature
Coefficient
|
-1.5%/K
|
Hygroscopic
|
slightly
|
Table 3-1
Properties
of (pure) CsI; compare with Phys. Rev. D50 (1994) 1261 and Figure 3-5.
The drawbacks of CsI are a high temperature gradient of -1.5%/K and
a slight hygroscopicity. Both properties require a temperature and climate
controlled surrounding for the calorimeter. This is necessary, anyhow, to
provide stable working conditions for the voltage dividers of the
photomultiplier tubes.
A short radiation length provides compactness due to a high stopping power for
both positrons and photons. This especially is valid for higher energies
(>10 MeV), when the positron, or electron respectively, loses energy by
bremsstrahlung rather than by ionization which initiates electromagnetic
showers[12].
Photons and positrons (or electrons, respectively) passing matter are losing
energy mostly due to electromagnetic processes. Photons may undergo Compton
scattering, produce photoelectrons or create electron-positron pairs depending
on the energy. Positrons can ionize, emit bremsstrahlung or annihilate with an
electron. The cross section for these individual processes depends on the
particle energy, as well as the density and the atomic number of the material.
Figure 3-3 shows the energy dependence of processes responsible for the energy
loss of photons.
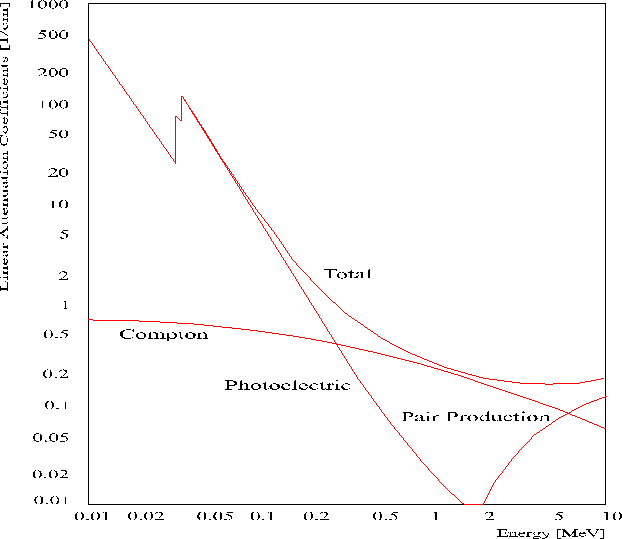
Figure 3-3 Linear Attenuation Coefficient of CsI as a function of photon
energy. At larger energies (beyond the scale of this figure), where the pair
production process is dominating, the energy loss of photons and electrons is
similar.
For energies much higher than the pair energy (1.022 MeV), pair production is
the dominant process. At those energies the daughter particles will again be
able to undergo the above mentioned electromagnetic processes. In this way an
electromagnetic shower emerges. Such a shower can be characterized using the
position of the shower maximum and the average shower width. In average a
shower appears to be a cone; but can also have extreme distributions, i.e. when
a daughter particle traverses several crystals without interactions and
consequently deposit energy in a remote crystal. Some examples of these
untypical distributions are shown in Figure 3-4.
Due to multiple scattering of shower particles there is also a notable lateral
energy deposition. This distribution scales well with the Molière
radius. In order to avoid intercalibration effects due to the summing over
several crystals and to keep the energy loss low, a small Molière radius
is desired.
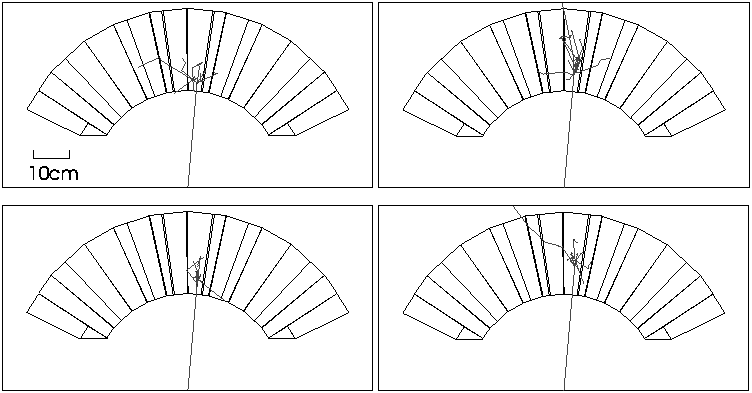
Figure 3-4 Untypical shower distributions of 50 MeV photons impinging the
CsI calorimeter
[12] see section 7.4 for a more detailed discussion




















