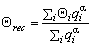previous next Up Title Contents Index

4.2 Angular Resolution and Track Reconstruction

For a reliable kinematic analysis a good angular resolution is desirable, since the decay angles are directly related to the particle energies. It is helpful to reconstruct the particle track which for photons is only accessible through the energy distribution within the calorimeter. The principle of photon track reconstruction was cross checked with the wire chamber information for positrons, which will be shown in Figure 4-7.

The theoretical angular resolution was obtained by comparing the reconstructed tracks with the coordinates of the thrown particle in simulation. The shower reconstruction routine simply is looking for the mean of the shower distribution in order to determine the point of incidence and compare it with the thrown angle in the simulation. Positrons, as well as photons, were thrown uniformly over the detector array of 44 crystals; then a cut that required the shower maximum to be within the innermost crystals was applied. This cut notably reduced the low energy tail - due to shower leakage - notably (see Figure 7-10 and sect.7.5). Since a shower normally develops in a cone, besides the crystal containing the largest fraction of energy some neighbouring truncated pyramids are affected as well. Thus the portion of contributed energy of each affected crystal has to be weighted with an exponent a <1. Consequently the formula to reconstruct the point of incidence becomes

,

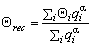where qi is the fraction of deposited energy in the i-th crystal Ei/Etot. The same applies for the f -direction.

Now the proper weighting factor a had to be found: An angle w was defined describing the deviation of the reconstructed position from the thrown position. It is given by

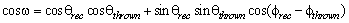(4.a)

This angle was minimized by varying a which resulted in a value of 0.71 for a at an angular resolution of 3.6°.

Weighting factor a
Angular Resolution
0.35
4.2°±0.3°
0.71
3.63°±0.2°
1.00
3.77°±0.2°

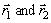Since electromagnetic showers develop as a symmetrical cone with definite radius only in average, an investigation of accounting for non-uniform shower distributions by applying a dipole-like correction with an additional weighting of the angular distance to the shower centre has been studied. Since the distance s of the two vectors in spherical coordinates is given by

,

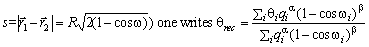where qi is the fraction of energy and cos( w i) the angular distance between the ith crystal and the mean shower depth.

The improvement was marginal (3.61° angular resolution with a =0.53 and b =1.9) and thus the initial method has been retained unchanged.

T. Noble [Nob90], working with rectangular NaI(Tl)-crystals, reports a weighting factor a of 0.55. This can be understood by the geometry of an electromagnetic shower. A hexagonical pyramid that contains the largest energy fraction of the shower is more likely to be the crystal which first was hit by the initial particle than for the case of a rectangular crystal. Consequently, for a planar geometry, neighbouring crystals are playing a more important role and, hence, the weighting factor must be lower.

Ideally one would expect a uniform distribution of the reconstructed positions as the thrown particles are distributed uniformly. But, due to the considerable size of the crystals, showers that are distributing energy over a large fraction of the detector cannot be reconstructed precisely. The average angle between two crystal centres is about 12°.

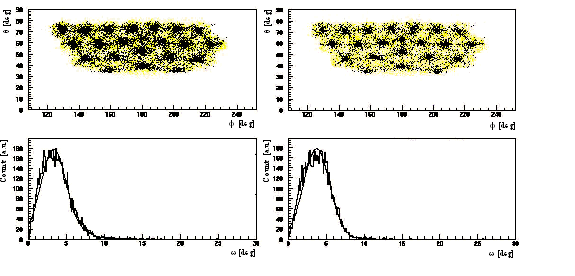
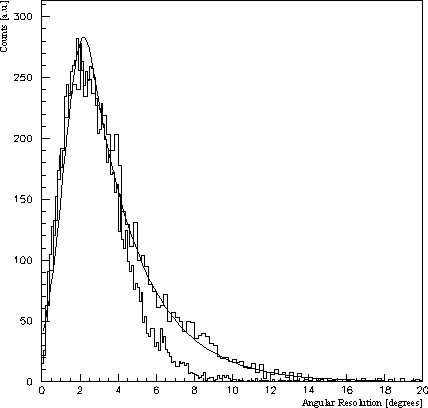
Figure 4-4 Comparison of the position reconstruction (above) and angular resolution respectively(below), for the found optimal weighting factor (left) and weighting factor 1 (right).

The main limitations for obtaining a better angular resolution (besides the granularity) are shower fluctuations that lead to a large uncertainty of the reconstructed position of incidence. This can be demonstrated by trying to reconstruct a pencil-like photon, or positron, beam. If those simulated tracks are off a crystal's centre, without applying weighting the distribution is small, but the reconstructed point of incidence deviates considerably. With a weighting factor the error for the reconstructed incidence is lower, but the distribution gets wider, because neighbouring crystals occasionally are receiving a major fraction of the total energy. Hence, in the q - f -plot the crystal positions are still recognizable (Figure 4-4). The tail to higher angular differences is due to shower fluctuations. Better results can be obtained if one restricts to showers starting close to a crystal centre, but this compares to a too restrictive cut that requires more than 80 per cent of the shower energy in a designated crystal.

Differences between the shower distributions of photons and positrons can also be found in studying the angular resolution. Therefore the theoretical angular resolution for positrons and photons of 10, 30, 50 and 70 MeV was determined. This is summarized in Figures 24 and 25. There the angular resolution, defined as the angle between the thrown and the reconstructed trajectory, for positrons and photons is plotted for ten values of a .

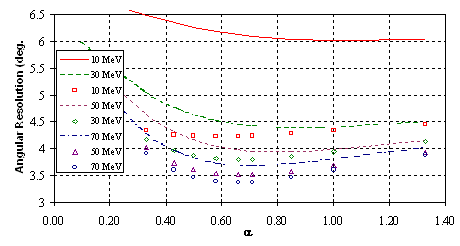
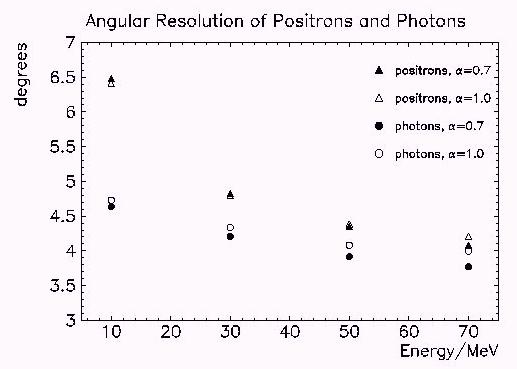
Figure 4-5 Comparison of the angular resolution for photon (symbols) and positron (lines) induced showers obtained using different weighting factors.

Figure 4-6 Comparison of the angular resolution of photons and positrons at different energies. See text for a detailed interpretation.

The comparison reveals two obvious results. For both types of particles the resolution improves with higher energy, which even is more pronounced with positrons. At higher energies the showers will start deeper inside the crystal volume and due to its shape the shower energy is spread over a lesser number of crystals. Furthermore the shower cone becomes smaller. Positrons have a lower angular resolution in comparison with photons for the same reasons; they initiate showers earlier. Another difference, regarding photon and positron induced showers, is the optimal value for the weighting factor a . For photons its value varies slightly from 0.58 at 10 MeV to 0.66 at 70 MeV while for photons at 10 MeV a =1 seems to be best. The optimum factor for photons then decreases to 0.71 for 70 MeV. The factor a is considered to be directly proportional to the shower cone radius divided by the angle between the crystal's front face and its sides. If the shower would develop in the same way as the crystal becomes wider a should be 1. This means that low energy positrons must have a larger shower cone than more energetic positrons. The converse change for photons can be explained with a deeper penetration of the crystals in general (see also Table 7-2). During the 1996 beam time two small wire chambers were used for beam monitoring. They also acted as an interface between data and simulation. So the theoretical angular resolution could be compared with the measured one. Using positrons the wire chambers allowed to determine the intersection point with a precision of 0.2 mm, approximately. With a 70 MeV positron beam of 1 cm diameter impinging the array perpendicularly an angular resolution of 3.8°±0.2° was obtained. This result cannot be compared directly to the simulated value given above, since the array was illuminated uniformly there. Trying to simulate the conditions during data taking the reconstruction of the impact point peaked at the same position as for the data. The slower fall-off of the tail can be explained with a non-uniform beam distribution due to an allowed beam divergency of 2°.

Figure 4-7 Comparison of measured and simulated angular resolution. The histogram obtained from 1996 beamtime period was superimposed by a Gauss-exponential curve to guide the eye. For the tail difference see text.

previous next Up Title Contents Index