





Prior to the construction of the detector Monte Carlo simulations have been studied in order to specify the requirements for the individual detector modules, study background processes, trigger layout, etc. The concept for the detector was approved by comparing results from the simulations codes GEANT, EGS4 and ITS [Poc89].

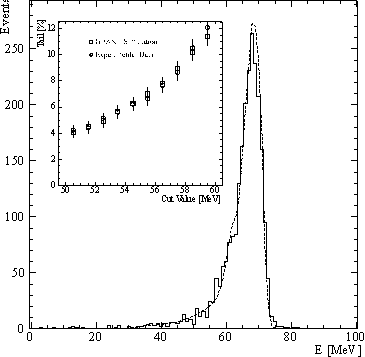
Figure 4-1 Comparison of data (histogram) and simulation (dashed curve). The insert emphasizes the fraction of the integral below the cut value divided by the total integral. Picture taken from [Bro96]. With the delivery of the first CsI crystals measurements and simulations could be compared and modifications of the simulation were included in the study. Results from test-beam periods and crystal tomography data have been implemented. The calorimeter simulation also includes wrapping materials, photon statistics and the position dependence of the light yield. Very good agreement between measured and simulated results, especially in the tail region, was obtained [Ass95]. As a conclusion, simulations assist reliably in data analysis, including calibration of the individual modules and determination of correction factors (as will be seen in ch.7).

Figure 4-2 Photograph taken during the CsI assembly of the sphere showing radial adjustment.
The electromagnetic calorimeter was optimized for similar response to both ~68 MeV photons and ~69 MeV positrons, for compactness, high granularity and high stopping power. This is best accomplished by a sphere consisting entirely of sensitive material. In order to approach an optimal detector as close as possible the entire support structure is located on the periphery of the calorimeter. Hence, apart from 200 µm of wrapping between the crystals, all of the calorimeter volume is sensitive and no heavy material is placed between the target and the CsI crystals. This minimizes energy degradation - or even showering - in front of the calorimeter. Photons or positrons leave the target, pass the wire chamber and the hodoscope and start showering after some centimetres within the calorimeter. The positrons also can lose up to 6.4 MeV in the target and generate a signal in the wire chamber and the hodoscope.
The processes involved in the energy loss in the calorimeter for both kinds of particles are similar. Both particles initiate a repetitive pair-production and bremsstrahlung process. Positrons are likely to start the shower earlier due to scattering and bremsstrahlung losses in the heavy CsI medium. This affects the acceptance, the angular resolution and the low-energy tail due to leakage.
The acceptances for obtaining the pion beta decay and the calibration process p +->e+ n e will differ slightly. One reason is a lower probability to detect both photons from the p 0 decay as opposed to a single positron close to the veto crystals. Another source of deviations is the slightly different shower development for positrons and for photons that affects the acceptance after energy cuts; this again enhances the positron acceptance. Positrons lose energy during their passage through matter. This energy is dependent on the emission angle, therefore the acceptance will slightly decrease at larger angles. The absolute differential acceptance obtained from simulations, which include the above mentioned points, can be viewed in Figure 4-3.





