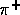 and suppose q,
and suppose q, 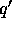 , p and k
are the 4-momenta of the
, p and k
are the 4-momenta of the  ,
, 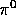 ,
,  and
and 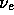 respectively. The relations below follow from momentum conservation:
respectively. The relations below follow from momentum conservation:




Consider the beta decay of 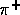 and suppose q,
and suppose q, 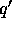 , p and k
are the 4-momenta of the
, p and k
are the 4-momenta of the  ,
, 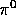 ,
,  and
and 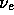 respectively. The relations below follow from momentum conservation:
respectively. The relations below follow from momentum conservation:
with
where
The expressions for the energies and momenta of the final state particles are obtained by considering the 2-body processes below:

with final state masses 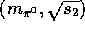 ,
,
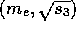 and
and
 respectively [Byc-73]. The explicit calculations
in the rest frame of the decaying
respectively [Byc-73]. The explicit calculations
in the rest frame of the decaying  reveal:
reveal:
and
The momenta follow from the energy-momentum relation
The kinematic constraints on the final state particle energies are derived as
follow: from equation ( ),
), 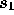 reaches a
minimum when
reaches a
minimum when
To arrive at the relation ( ), one writes
), one writes
where  is the angle between the 3-momenta.
Equation (
is the angle between the 3-momenta.
Equation ( ) goes through a minimum at
) goes through a minimum at 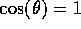 .
This
means that the 3-momenta of
.
This
means that the 3-momenta of 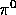 and
and 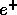 are collinear. Suppose
that the minimum is some value a to be specified. One gets:
are collinear. Suppose
that the minimum is some value a to be specified. One gets:
which leads immediately to:
where 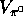 and
and 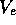 are the magnitudes of the velocities of
the neutral pion and the electron respectively. Setting
are the magnitudes of the velocities of
the neutral pion and the electron respectively. Setting
Taking the derivative of equation ( ), the
minimum is reached at
), the
minimum is reached at  where
where  :
(
:
( ) is proven and in addition, the neutral pion
and the positron have the same velocity as can be seen from
(
) is proven and in addition, the neutral pion
and the positron have the same velocity as can be seen from
( ). From (
). From ( ),
),
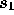 reaches a maximum when the neutrino is born at
rest. It is straightforward to establish the kinematic constraints on
reaches a maximum when the neutrino is born at
rest. It is straightforward to establish the kinematic constraints on
 and
and  . Gathering all the information together:
. Gathering all the information together:
The above relations together with
equations ( ,
,  and
and  ) give the allowed
energies of the neutral pion, the positron and the neutrino as:
) give the allowed
energies of the neutral pion, the positron and the neutrino as:
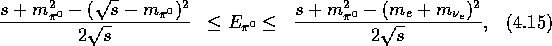
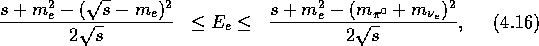
and

Neglecting the neutrino mass, the explicit calculations show:

The maximum kinetic energy of the 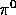 is about
is about  .
Because of this recoil energy, the momenta of two gamma rays which
originate from the decay of
.
Because of this recoil energy, the momenta of two gamma rays which
originate from the decay of  are not necessarily collinear. Their
opening angle can be computed as follows:
are not necessarily collinear. Their
opening angle can be computed as follows:
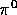 is at rest, the two gammas have opposite
momenta and same energy
is at rest, the two gammas have opposite
momenta and same energy
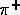 :
:
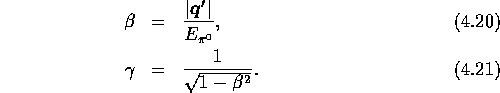
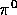 to a frame
where the momentum
to a frame
where the momentum 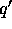 of the neutral pion lies
along the z-axis gives the 4-momentum of one of the gamma rays
of the neutral pion lies
along the z-axis gives the 4-momentum of one of the gamma rays
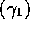 as:
as:

 and
and  are the polar angles of the gamma in
the rest frame of
are the polar angles of the gamma in
the rest frame of 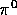 where the momenta of the gammas are isotropic
with
where the momenta of the gammas are isotropic
with 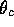 and
and 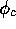 satisfying the conditions:
satisfying the conditions:
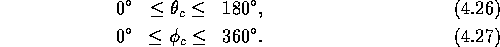
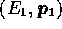 of the
gamma in the rest frame of
of the
gamma in the rest frame of  , one performs the rotation
, one performs the rotation
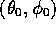 as follows, with
as follows, with  and
and 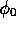 being the polar angles of the momentum
being the polar angles of the momentum 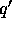 of
of  in the rest frame of
in the rest frame of 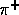 :
:
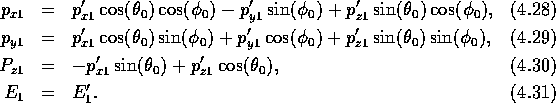
 of the
second gamma follow from space reflection:
of the
second gamma follow from space reflection:

 shows the distribution of the opening angle
of the two gamma rays, and the energy spectrum of one of the photons
is displed in figure
shows the distribution of the opening angle
of the two gamma rays, and the energy spectrum of one of the photons
is displed in figure  .
.



