




The differential decay width is:
where the matrix element is
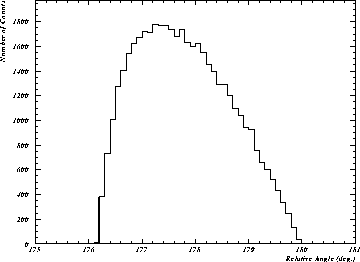
Figure: The opening angle between the two gamma rays
from the 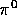 decays. The directions of the gamma rays deviate from collinearity by at
most
decays. The directions of the gamma rays deviate from collinearity by at
most  due to the recoil energy of the
due to the recoil energy of the 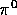 .
.
The hadronic matrix element 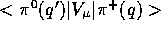 can only be a
vector as explained in chapter one. With the similar method used to write
down equation 1.42, the hadronic matrix element is:
can only be a
vector as explained in chapter one. With the similar method used to write
down equation 1.42, the hadronic matrix element is:
with
Equation ( ) follows from the fact that since there is no
spin,
) follows from the fact that since there is no
spin,  and
and  are the only vectors available
to construct the matrix element. The CVC hypothesis requires that
are the only vectors available
to construct the matrix element. The CVC hypothesis requires that

Figure: The energy spectrum of one of the
gamma rays originating from the decay of the 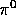 . The spread of this energy
reflects the spread in the recoil energy of the
. The spread of this energy
reflects the spread in the recoil energy of the 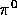 .
.
which leads to
In the exact isospin symmetry, 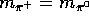 hence
hence
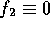 . The square matrix element is:
. The square matrix element is:
where
Using some trace theorems [Hal-84], it is a straightforward exercice to show that
In equation ( ), the terms proportional to
), the terms proportional to 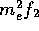 are
negligible compare to the rest due to the electron mass. In addition,
since the range of
are
negligible compare to the rest due to the electron mass. In addition,
since the range of  is small
is small  ,
,
 is replaced by its value at
is replaced by its value at 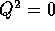 . However,
. However,  is
fixed by the CVC hypothesis:
is
fixed by the CVC hypothesis:
as was demonstrated in chapter one. With all these simplifications, the matrix element becomes:
At this point, the decay width is written as:
where
and
The above equation can be written as:
One may write  more elegantly as:
more elegantly as:
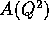 and
and  need to be isolated and calculated. To that end, one
contracts (
need to be isolated and calculated. To that end, one
contracts ( )
with
)
with  and with
and with
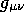 . The results are two equations which are quickly solve to
get:
. The results are two equations which are quickly solve to
get:
and
After the isolation of 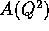 and
and 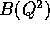 , the integrations can be
performed with the aid of the following properties of the
, the integrations can be
performed with the aid of the following properties of the
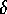 -function:
-function:
and
with
 is the step function. The
integral (
is the step function. The
integral ( ) reduces to:
) reduces to:
where k has been replaced by Q-p. One gets:
and
Putting all this together,
Integrating over the 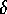 -function:
-function:
To get the limits  and
and  , one realizes that after the
, one realizes that after the
 -function integration, (
-function integration, ( ) becomes:
) becomes:
Since
equation ( ) sets the range of integration over
) sets the range of integration over 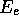 which
is determined as follows: solve (
which
is determined as follows: solve ( ) for
) for
 and use the
condition (
and use the
condition ( ) to get:
) to get:
One arrives at the discriminant
and finds the roots
from which the desired range of  is obtained:
is obtained:
Finally, the integration ( ) is carried out to get
) is carried out to get 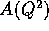 :
:
With similar approach,
The decay width can now be written as:
From  ,
,
and from the energy-momentum relation
where  is the pion mass difference:
is the pion mass difference:
In addition,
Furthermore,

and

The decay width now appears as:
where small terms of the order 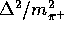 have been
neglected. It is useful to introduce a variable z and a
parameter
have been
neglected. It is useful to introduce a variable z and a
parameter  such that:
such that:
and
Finally, the decay width is obtained as:
where
It is straightforward to show that with 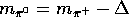 ,
,
The integration ( ) can also be carried out:
) can also be carried out:
Equation ( ) together with the main decay mode of the
) together with the main decay mode of the  ,
that is
,
that is 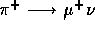 , gives the branching ratio of
the pion
beta process:
, gives the branching ratio of
the pion
beta process: 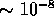 . The other decay channels of
. The other decay channels of  are
listed
below with their probability of occurrence in parentheses:
are
listed
below with their probability of occurrence in parentheses:



