 ) with
) with 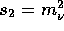 . Neglecting the neutrino
mass,
the muon kinetic energy in the rest frame of the pion is:
. Neglecting the neutrino
mass,
the muon kinetic energy in the rest frame of the pion is:




The energy of the muon in this 2-body decay is given by
equation ( ) with
) with 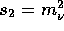 . Neglecting the neutrino
mass,
the muon kinetic energy in the rest frame of the pion is:
. Neglecting the neutrino
mass,
the muon kinetic energy in the rest frame of the pion is:
The matrix element of the decay is:
In this case, the vector contribution to the hadronic matrix element must vanish because of parity [Geo-84]. The axial vector contribution is parametrized as:
One notes in passing that if the pion were massless, the axial current would be conserved since:
in which case the pions could be identified as the Goldstone bosons associated
with the spontaneous breaking of chiral symmetry. Using Dirac equation and
zero mass for the neutrino, equation ( ) becomes:
) becomes:
Summing over final spin states and using some trace theorems:
The above expression together with the phase space factor gives, after integrating over fermion energies, the decay rate as:
In the case of a massless muon
(relativistic limit for instance), this decay would be forbidden: in
the relativistic limit, leptons are left-handed and antileptons are right-handed
due to the V-A structure of the interaction and in analogy to the case of
the neutrino discussed in chapter one. By considering the conservation of
helicity and angular momentum, this decay is forbidden.