and 
.
These parameters are
used to calculate an angle of incidence correction which is applied
(dx in Equ. 5.1) to the reconstructed
shower origin coordinates. This correction is important because the
incident particles are not necessarily normal to the surfaces of the
crystals in the detector arrays. Such a particle, with a non-zero
transverse momentum component, can result in a shower origin which is
offset from the actual impact point of the particle with the calorimeter
surface.
By assuming that the target is a point source, the angle of incidence of the particle can be calculated for each event. This approximation holds as long as the actual target size is small compared to the distance between the target and detector arrays.
For the NaI detector, the angle of incidence correction is calculated
along the two directions in the plane of the front face of the array,
and 
. The technique used is similar to the one
suggested by A. Bay et. al. [1]. The shift 
(or 
) is applied according to
Fig. 5.2, where is related to the
electromagnetic shower penetration depth and is a function of energy.
From Fig. 5.2 one can see that
.
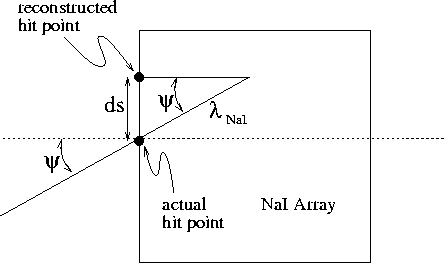
Figure 5.2: Geometry used to calculate angle of incidence corrections
to shower reconstruction coordinates in NaI array.
For the CsI detector, which has a spherical geometry, the angular
correction is applied to produce a shift in the 
and
directions, which are also along the front face of the array.
First, the angle of incidence 
with the normal to the detector surface
is calculated in each direction and , as shown in
Fig. 5.3.
Next, because the linear correction x is small compared to the distance
to the target r, one
can assume that 
. Assuming that the linear
correction x is much less than the sphere radius R, one can see from
Fig. 5.3 that
.
Finally, the angular correction
in both the and directions takes the form
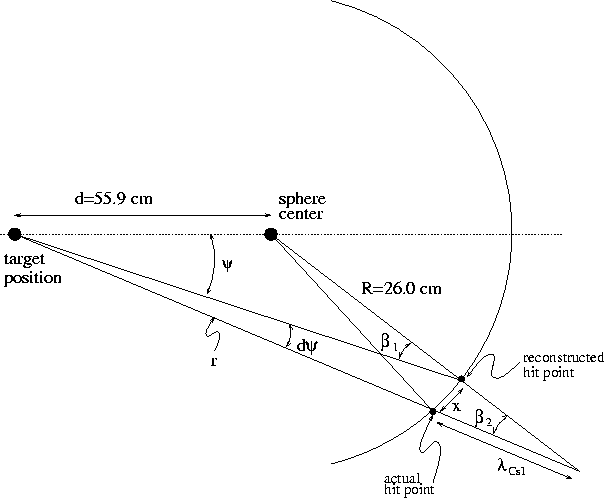
Figure 5.3: Geometry used to calculate the angle of incidence correction
to the reconstructed shower coordinates in the CsI array.
The values of the shower depth parameters and
have been chosen for optimal average angular resolution. Figure 5.4
shows the plots of average angular deviations 
plotted
against 
,
for 55-83 MeV photons from the reaction 
in the GEANT
simulation. One can see that the
optimal values are 
cm and 
cm. These penetration
depths reflect the fact that the NaI crystals have a lower atomic number than the
CsI crystals, shown in the larger value for .
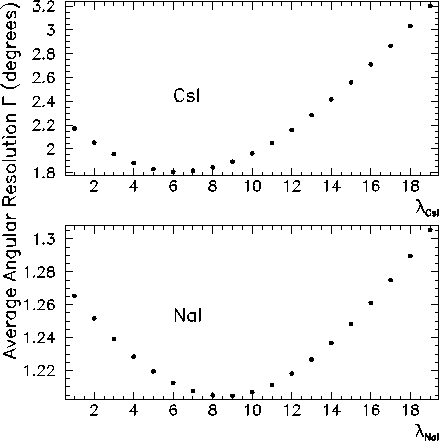
Figure 5.4: Average angular deviation plotted against the shower
penetration depth parameter , for the CsI array (top panel)
and NaI array (bottom panel).
Finally, the event-by-event angular deviations 
are plotted in
Fig. 5.5, with and without the angle of incidence corrections.
It is clear that there is a significant improvement with the inclusion of
the correction. The CsI decreases from 2.3
to
1.8, and the NaI from 1.3 to 1.2.
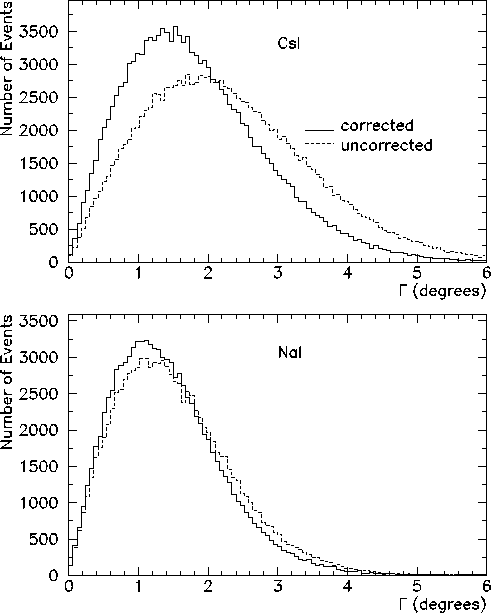
Figure 5.5: Angular deviations , with and without the angle of
incidence corrections, for the CsI array (top panel) and NaI array
(bottom panel).