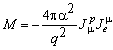 .
.





Fermi's idea was to compare the four-fermion point interaction as an interaction of two currents in analogy to the electromagnetic interaction. For proton-electron scattering, for instance, the matrix-element can be written as
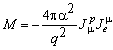 .
.
J represents the current densities for proton and electron,
respectively, and q the momentum transfer. Here the proton couples to
the electron with the strength a which is known as the fine structure
parameter
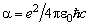 .
Fermi consequently introduced the weak current that decomposes into a hadronic
and a leptonic current. Using the picture of second quantization (field
quantization) the transition operator can be pictured as annihilator of the
particle of the right hand side and creator of the particle on the left hand
side. In the theory of four-fermion point interaction two particles are
transformed simultaneously and therefore one writes the matrix element [Fey58]
.
Fermi consequently introduced the weak current that decomposes into a hadronic
and a leptonic current. Using the picture of second quantization (field
quantization) the transition operator can be pictured as annihilator of the
particle of the right hand side and creator of the particle on the left hand
side. In the theory of four-fermion point interaction two particles are
transformed simultaneously and therefore one writes the matrix element [Fey58]
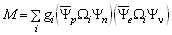 .
.
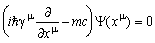 .
.
In order to describe observables (which must be real expressions) in the Dirac
theory[4], bilinear forms like
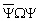 with W being a 4x4 hermitean matrix, have to be generated. This results
in 16 linear independent basic matrices which are be classified as follows
with W being a 4x4 hermitean matrix, have to be generated. This results
in 16 linear independent basic matrices which are be classified as follows
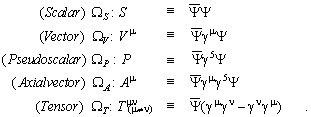
 ,
,
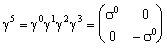 (i=1,2,3)
(i=1,2,3)This set of matrices guarantees that solutions of the Dirac equation also will fulfil Lorentz-invariance. The parity operator can be introduced by building the chiral projection operators:
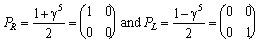
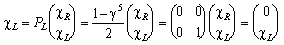
(and analogous for the right-handed component).
The chiral symmetry was introduced by Feynman and Gell-Mann to account for parity violation, which was not known to Fermi. It can be shown that only V- and A-coupling correctly describe the maximal parity violation, since
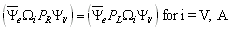 .
.Using this, the matrix element becomes
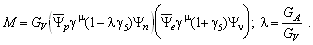
A textbook example to verify (V-A) theory is the calculation of pion-decay into leptons, since parity violation in pion and muon decays was observed along with the nuclear b -decay measurements mentioned above. Following the four fermion interaction picture with replacing the pion by a hadronic current of an up-quark changing into a down quark in the single-point, which demands universality of the weak interaction. It claims an universal coupling constant for all lepton decay and scattering processes (the equivalence of the coupling strength for weak interacting hadronic particles is expressed in the CVC hypothesis). In this example of a pion decay into leptons the conservation of angular momentum then determines the spin direction of the charged leptons, which have to be opposite to the (anti-)neutrino since pions do not carry spin. Finally, regarding conservation of momentum, the charged leptons have the same chirality as the neutrinos. The helicity of the neutrino must be -1. Hence, neutrino helicity determines the chirality of the charged lepton. Due to the fact that the probability to find a massive particle with unfavourable helicity goes with 1- b , the rate of the decay p +->e+ n e should be lower than for p +->µ+ n µ. With the approximation me2/m p 2 <<1 the ratio of decay rates turns out to be
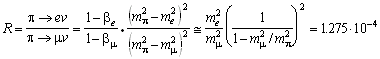 ,
,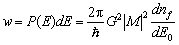 .
.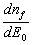 represents the density of final state, M the transition matrix and
G a combination of coupling constants.
After a short calculation (see [Kal72] for example) and integration over the
electron energies one obtains for the decay width:
represents the density of final state, M the transition matrix and
G a combination of coupling constants.
After a short calculation (see [Kal72] for example) and integration over the
electron energies one obtains for the decay width:
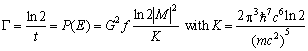 .
.
The function f comprises the kinematic terms of the integrated state
density and the electromagnetic interaction of the electrons and t represents
the half-life. The connection of [florin]t-values, which are used to classify
the b -decays, to the coupling constant one obtains after calculating the
matrix element. Here the simplest case is a transition without a flip of the
nucleon spin (I) and thus with anti-parallel electron and neutrino
spins. An example of this pure Fermi transition is the inverse b -decay
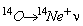 .
In order to calculate the matrix element one forms an isospin T=1
triplet of isotopes with the atomic number A=14. The isospin positions
Tz are calculated assuming a
.
In order to calculate the matrix element one forms an isospin T=1
triplet of isotopes with the atomic number A=14. The isospin positions
Tz are calculated assuming a
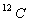 core
with additional nucleons
core
with additional nucleons
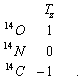
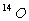 decay is an example of a pure Fermi decay. Hence, the calculation of the matrix
element M simplifies to sum over isospin T with
Tz=1 in the initial state and
decay is an example of a pure Fermi decay. Hence, the calculation of the matrix
element M simplifies to sum over isospin T with
Tz=1 in the initial state and
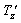 =0
in the final. One obtains
=0
in the final. One obtains
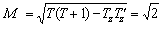 and finally
and finally
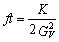 ,
,
since terms other than of vector type do not contribute Nuclear b -decays are classified according to their log([florin]t)-values:
| Type
of transition
|
D I
|
parity
|
log([florin]t)
value
|
| super-allowed
|
0
|
+
|
~
3.5
|
| allowed
|
0,1,
no 0->0
|
+
|
~
5.7
|
| (multiple)
forbidden
|
0,1
or >1
|
-
|
>
7.5
|
Before one can extract the exact coupling constant from the [florin]t-value, corrections have to be taken into account (see [Wil94,97] for a comprehensive discussion. Those are
* radiative corrections d r (from QED and QCD) of 3-4%
* nuclear correction d c of 0.2-1%
* screening effects due to Coulomb interaction with the core
Thus one writes f't = [florin]t (1+ d r) (1- d c). The rate of the pure Fermi nuclear b -decay is directly related to the vector coupling constant assuming the CVC hypothesis that claims the coupling to the hadronic current independent from the participating particles. Pions and nucleons therefore can be treated equally within this theory. Furthermore the standard model assumes the existence of an universal coupling constant for all weak processes. Hence, measuring the decay rate of a b -decay, GV can be obtained or, taking Gµ from the muon decay, universality of the weak interaction can be tested.
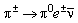 can be described in the same way. Opposed to the nuclear b -decay neither
inner nor outer nuclear corrections have to be taken into account; only
radiative corrections (calculable with an accuracy of 0.2% [Sir92]) have to be
considered. Thus the pion beta decay rate can be calculated with higher
precision. A simple estimation of the pion beta decay rate can be done using
the Sargent rule that asserts the dependence of the decay probability over time
to the fifth power of the energy[Per86]. This gives
can be described in the same way. Opposed to the nuclear b -decay neither
inner nor outer nuclear corrections have to be taken into account; only
radiative corrections (calculable with an accuracy of 0.2% [Sir92]) have to be
considered. Thus the pion beta decay rate can be calculated with higher
precision. A simple estimation of the pion beta decay rate can be done using
the Sargent rule that asserts the dependence of the decay probability over time
to the fifth power of the energy[Per86]. This gives
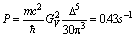 ,
,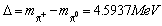 [Cza93]). With an exact calculation including radiative corrections one gets
after Källén [Kal72]:
[Cza93]). With an exact calculation including radiative corrections one gets
after Källén [Kal72]:
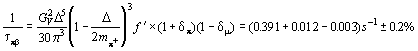 .
.(A more recent calculation by Sirlin [Sir92] gives (0.3996±0.0006) s-1).
Here the function f' is representing the integrated state density including electroweak corrections, d p the radiative corrections for the p of 0.012, and d µ.represents the radiative correction for the µ+->e+ n edecay. With the pion lifetime of 26.03 ns this is equivalent to a branching ratio (BR) of 1.031*10-8 or a ratio of 0.838*10-4 compared to our calibration decay p +->e+ n e .





