2.1.2 The Standard Model of Electroweak Interactions
In analogy to the isospin of the strong interaction one classifies the known
fundamental particles accordingly to their weak isospin TW.
Since the weak interaction is maximum parity violating they form a left-handed
doublet that carries weak charge and a right-handed singlet that does not. The
latter therefore is identified with the projection
.
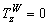Table 2-2 The generations of quarks and leptons in the standard model of
electroweak interaction.
The logical consequence of the analogy of the weak interaction to
electromagnetism is the advent of a particle[5]
mediating the weak force like the photon mediates the electromagnetic
interaction with the coupling constant a . The coupling constant of the
weak interaction then is GV, furthermore the electric charge
conservation law corresponds to the conservation of the vector current. Within
the electroweak theory the beta transition is described using a virtual gauge
vector boson (W-Boson) that couples the hadronic current to the leptonic
current with equal strength. For a vanishing momentum transfer
q2<< M2, where represents the mass
of the W, the coupling constant gW of the W-Boson is directly
related to GV via
.
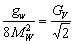The success of formulating local gauge invariance with non-Abelian symmetry
groups, i.e. SU(2) - introduced by Yang and Mills - and the maximum chiral
symmetry breaking of the weak interaction led to the electroweak interaction
theory that was independently formulated by Weinberg and Salam based on
previous work of Glashow [Gla61]. Herein the weak isospin group SU(2) was
combined with the weak hypercharge group U(1) in order to account for charge
conservation.
Characteristic is the spontaneous symmetry breaking of the SU(2)xU(1) group by
the Higgs field that explains the short reach of the weak interaction. This led
to the prediction of the intermediate massive Vector-Bosons and their total
chiral asymmetry. On top of that the U(1) symmetry remained unbroken and the
(massless) intermediate Vector-Bosons was identified as the photon. This
fundamental concept of gauge invariance and spontaneous symmetry breaking was
verified later; at first, theoretically, when t'Hooft proved the
renormalizability in 1971 before the predicted neutral currents were found
(1973). Finally, the triumph for the Glashow-Weinberg-Salam theory of
electroweak interaction was the discovery of the W±- and
Z0-Bosons (1983). (Up to now only the Higgs-Boson remained
undiscovered.)
The CVC Hypothesis in the framework of the SU(2)xU(1) electroweak group is a
direct consequence of the Noether theorem that claims a conserved quantity for
any continuous symmetry. Unlike axial transformations, vector rotations in
hadronic flavour space leave the vacuum invariant and therefore a conserved
vector current must exist.
[5] As seen before this necessarily has to be a
boson obeying vector coupling.
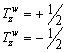
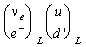
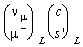
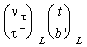
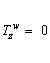
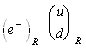
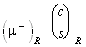
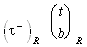
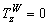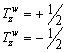
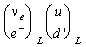
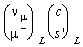
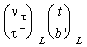
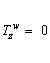
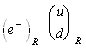
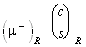
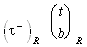
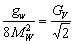