In general all measured or calculated decay rates do include radiative decays - regardless of the origin of the emitted photon. Their relevance for the upcoming measurement of the pion beta decay rate are twofold: i) Neglected radiative p +->e+ n µ decays would result in an additional uncertainty due to an underdetermined calibration process and ii) four-fold coincidences of pairs of µ+->e+ n eµ( g ) decays could fake an p b event. For both cases the relative strength and the emission angle between photon and charged particle have to be recorded. Hence, the calorimeter acceptances and a possible cluster recognition algorithm had to be studied.
In order to measure the exact p +->e+ n e decay rate also the radiative mode has to be included. This requires an identification of the actual decay process and a determination of radiative decays. The most likely process is the p ->µ->e chain with a 14% probability for the radiative decay µ+->e+ n eµ g (at a g threshold energy of 10 MeV [Cri61]). This is identified by the presence of a charged particle and a total energy of at most half the muon mass[20]. Since the signature of the p b event is determined by the presence of two photons with nearly identical energies, the p +->e+ n e peak clearly can be identified by an energy exceeding 55 MeV [Law98, Ass95]. Furthermore the difference in lifetime will give different signatures in the target.
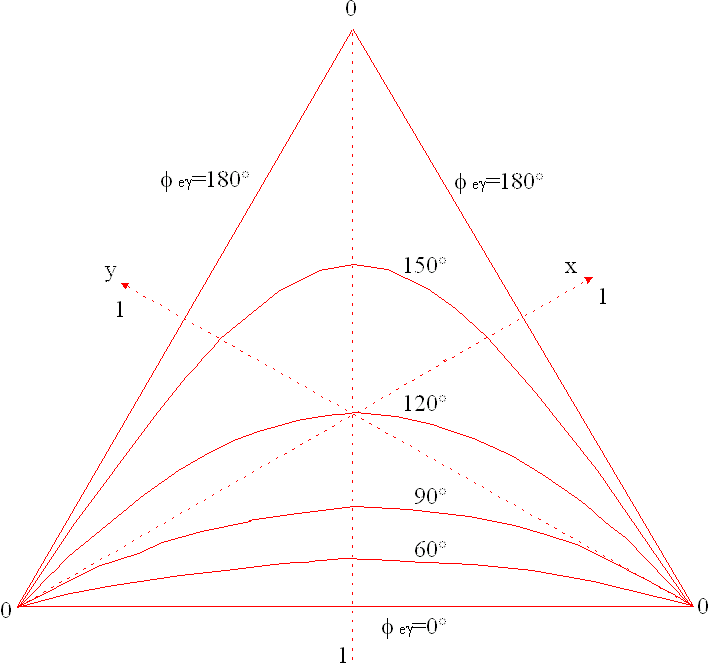
There are two major concerns regarding the decay p +->e+ n e g . In the unlikely case of a low energy neutrino it contributes to the background of the p b event. Due to the high chamber efficiency, the probability to have two clumps in opposite clusters without a charged particle identification calculates[21] -> to be 1.91*10-13. From kinematics it can be seen that only large emission angles, and therefore high photon energies, can be problematic. For lower angles a cluster summing algorithm, which will be explained in the subsequent section, will take care of radiative decays. The relative emission angle between positron and photon in the following is denoted as f .
(in the rest frame of the pion); y and z are equally defined for the electron
and the neutrino, respectively.
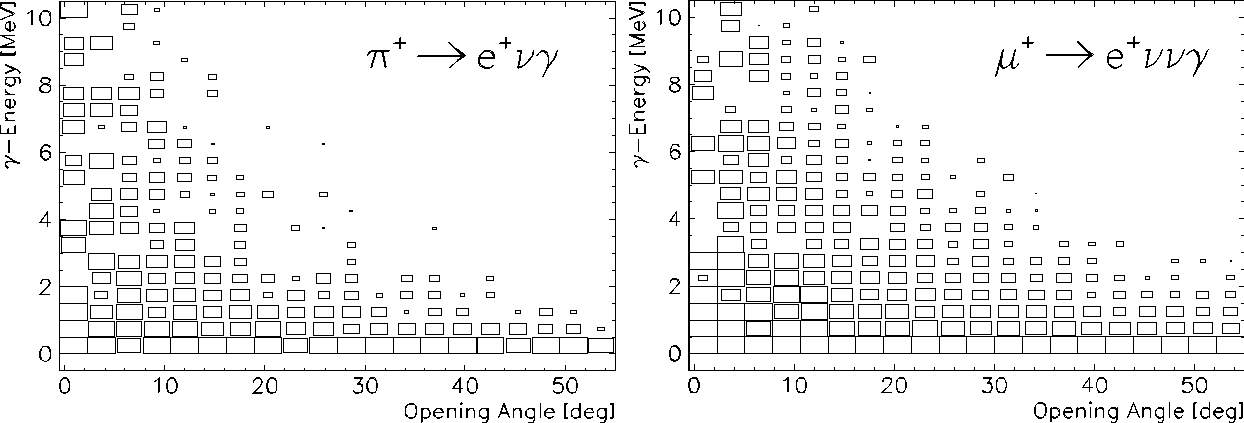
Regarding a simulation of the entire PiBeta calorimeter the relative acceptance for a p +->e+ n e g decay, for instance, with f >0° is at 86.2% while it reduces to 14.63% for f >30°. Since the µ+->e+ n e µ g process is generated with a much higher probability by bremsstrahlung processes the relative acceptance for f > 30° reduces to 0.032%. A similar reduction can be observed for cuts on the photon energy. The acceptances for radiative decays, relative to the correspondent non-radiative decays, are plotted below in Figure 5-2.
.
From this figure one can extract the relative calorimeter acceptances after applying kinematic cuts. It shall be summarized in Table 5-1.
[21] Here a cut on 50 MeV positrons and muons at a relative angle of >170° is assumed (this was chosen due the trigger thresholds and the kinematics of the p b -decay assuming 3 deg angular resolution). This leads to a BR of 0.47*10-8 for p +e+ n e g . For the parametrization of this calculation see [Bry82]. The charged particle tracking inefficiency comprises MWPCs and PV hodoscope and, hence, is about 4.0*10-5.