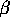The transition probability per unit time in nuclear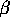 
-decay is
given by the golden rule:
where 
is the density of final states. The matrix element
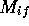includes a summation over all possible angular momentum states
of the leptons, over all final spin states of the nucleus and an
average over the spin orientations of the initial nucleus. For
convenience, the nucleus is assumed to be infinitely heavy and
therefore carries no energy but contributes the necessary recoil
momentum for the leptons [Hor-75].
The density of final states is:
where 
and 
are the number of states available to the
-particle and the neutrino in the momentum intervals p to
p+dp and q to q+dq respectively and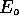 
is the
total energy carried by the leptons:
From the energy-momentum relations of the leptons, one has:
and
Neglecting the neutrino mass, the transition probability becomes:
where
and
The matrix element 
is given by equation (
) with
instead of G. One rewrites the matrix element as:
where the lepton matrix element 
is given by equation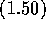 
and the hadron matrix element 
generally comprises a vector and an axial
vector contributions:
where V is the vector necessary to construct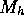 
.
With equation (), the transition
probability is:
where the factor 
, known as the Fermi Function, includes
among other things, correction factors such as screening effects by atomic
electrons and final state Coulomb interaction effects which are particularly
important at low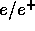 
energies and for high-Z nuclei. By integration the
transition probability over the 
energy spectrum, the decay rate is:
with
The product ft of the Fermi integral function f and the decay half
live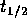 
is independent of kinematic effects and involves only
the matrix element:
where K is a product of fundamental constants. In cgs units,
