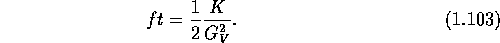Next: Motivation
Up: Superallowed Fermi Decay
Previous: Nuclear Beta Decay
Superallowed transitions are  -transitions between two members of
an isospin multiplet --- for instance a hadron A of spin zero decaying
into another spinless hadron with the same parity.
In this particular
case, the axial vector contribution to the matrix element
-transitions between two members of
an isospin multiplet --- for instance a hadron A of spin zero decaying
into another spinless hadron with the same parity.
In this particular
case, the axial vector contribution to the matrix element  vanishes because since there is no spin, it is impossible to construct
an axial vector out of two hadron momenta alone. These types of
transitions are pure vector interactions known as Fermi transitions and
can be used to test the CVC hypothesis. The coupling constant
vanishes because since there is no spin, it is impossible to construct
an axial vector out of two hadron momenta alone. These types of
transitions are pure vector interactions known as Fermi transitions and
can be used to test the CVC hypothesis. The coupling constant
 is the same as
is the same as  given in equation (
given in equation ( ). In
addition, the matrix element
). In
addition, the matrix element  which
is known as
which
is known as  for pure Fermi transitions, can be evaluated without
reference to the details of the nuclear wavefunctions. Since both
states belong to the same isomultiplet differing only in their values
of
for pure Fermi transitions, can be evaluated without
reference to the details of the nuclear wavefunctions. Since both
states belong to the same isomultiplet differing only in their values
of  (see equation (1.59)),
(see equation (1.59)), 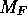 is the matrix element of the
isospin raising or lowering operator
is the matrix element of the
isospin raising or lowering operator 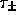 :
:

From angular momentum theory,

For all superallowed transitions of the type 

and
Bernward Krause
Mon Jan 15 14:57:06 MET 1996
 -transitions between two members of
an isospin multiplet --- for instance a hadron A of spin zero decaying
into another spinless hadron with the same parity.
In this particular
case, the axial vector contribution to the matrix element
-transitions between two members of
an isospin multiplet --- for instance a hadron A of spin zero decaying
into another spinless hadron with the same parity.
In this particular
case, the axial vector contribution to the matrix element  vanishes because since there is no spin, it is impossible to construct
an axial vector out of two hadron momenta alone. These types of
transitions are pure vector interactions known as Fermi transitions and
can be used to test the CVC hypothesis. The coupling constant
vanishes because since there is no spin, it is impossible to construct
an axial vector out of two hadron momenta alone. These types of
transitions are pure vector interactions known as Fermi transitions and
can be used to test the CVC hypothesis. The coupling constant
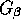 is the same as
is the same as  given in equation (
given in equation ( ). In
addition, the matrix element
). In
addition, the matrix element  which
is known as
which
is known as  for pure Fermi transitions, can be evaluated without
reference to the details of the nuclear wavefunctions. Since both
states belong to the same isomultiplet differing only in their values
of
for pure Fermi transitions, can be evaluated without
reference to the details of the nuclear wavefunctions. Since both
states belong to the same isomultiplet differing only in their values
of 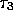 (see equation (1.59)),
(see equation (1.59)), 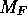 is the matrix element of the
isospin raising or lowering operator
is the matrix element of the
isospin raising or lowering operator 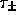 :
: