



Next: Pion Beam
Up: No Title
Previous: Superallowed Fermi Decay
Pion beta decay ( ) is one of the fundamental
semileptonic weak interaction processes. It is a transition between two
spin-zero members of an isospin triplet and is therefore analogous to the
superallowed pure Fermi transitions in nuclear beta decay. At tree level,
the rate of pure Fermi nuclear beta decay is directly related to the vector
coupling constant
) is one of the fundamental
semileptonic weak interaction processes. It is a transition between two
spin-zero members of an isospin triplet and is therefore analogous to the
superallowed pure Fermi transitions in nuclear beta decay. At tree level,
the rate of pure Fermi nuclear beta decay is directly related to the vector
coupling constant  and the nuclear Fermi matrix element
and the nuclear Fermi matrix element  . The
Conserved Vector Current hypothesis (CVC) predicts that the product
ft of the Fermi integral function f and the decay half live
. The
Conserved Vector Current hypothesis (CVC) predicts that the product
ft of the Fermi integral function f and the decay half live 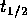 is a
universal constant given by:
is a
universal constant given by:

where K is given by equation ( ).
By comparing the vector coupling constant of the nucleon
beta decay
).
By comparing the vector coupling constant of the nucleon
beta decay  to that of the muon decay, it is possible to determine
to that of the muon decay, it is possible to determine
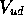 , the mixing matrix element between the u and d quarks.
Cabibbo universality relates
, the mixing matrix element between the u and d quarks.
Cabibbo universality relates  to the muon weak coupling constant
to the muon weak coupling constant
 via the CKM matrix element
via the CKM matrix element  [Shr-78]
[Shr-78]
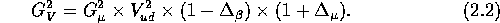
 is the muon decay coupling constant (see equation (
is the muon decay coupling constant (see equation ( ));
));
 and
and
 are the inner radiative corrections for
are the inner radiative corrections for  and
and
 decays respectively. The inner radiative corrections do not depend
on the electron energy. They do depend however on the details of the strong
interaction involved and the structure of the decay. In addition, they are
model-dependent and tend to diverge theoretically. They are relevant when
comparing different types of beta decay but act only to renormalize the
coupling constant when comparing the rates of beta decays of the same type.
In such cases, they are directly defined into the coupling constants themselves.
Some
decays respectively. The inner radiative corrections do not depend
on the electron energy. They do depend however on the details of the strong
interaction involved and the structure of the decay. In addition, they are
model-dependent and tend to diverge theoretically. They are relevant when
comparing different types of beta decay but act only to renormalize the
coupling constant when comparing the rates of beta decays of the same type.
In such cases, they are directly defined into the coupling constants themselves.
Some  nuclear beta decay processes, characterized
by the single parameter
nuclear beta decay processes, characterized
by the single parameter  are as follows:
are as follows:

For instance, the third reaction represents the transition from the ground
state of  with
with  to the first excited state
of
to the first excited state
of  with
with  .
.
Two types of nucleus-dependent corrections must be applied to
equation ( ) in order to extract
) in order to extract 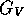 from the measured
decay rates: the phase
space dependent radiative corrections
from the measured
decay rates: the phase
space dependent radiative corrections  to the statistical
rate function f
to the statistical
rate function f  and the nuclear structure dependent
corrections
and the nuclear structure dependent
corrections  to the matrix element
to the matrix element 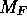
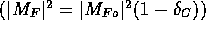 . The uncorrected Fermi matrix element
. The uncorrected Fermi matrix element
 is given by equation (
is given by equation ( ).
Taking into account the corrections
).
Taking into account the corrections  and
and  and the matrix
element of equation (
and the matrix
element of equation ( ), the nucleus
independent ft value becomes
), the nucleus
independent ft value becomes
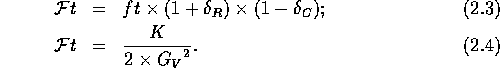
where the uncorrected Fermi integral function f and the decay half live
t are given by equations ( ) and (
) and ( ). The
empirical values of
). The
empirical values of  are determined from the
are determined from the 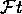 values.
values.
The outer radiative corrections  are model-independent and uniquely
specified.
are model-independent and uniquely
specified.
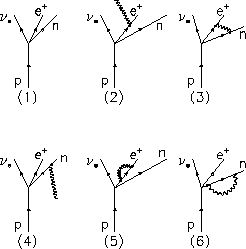
Figure: Feynman diagrams
for the beta decay of a point nucleon: (1) no
radiative correction; (2)--(6) first order radiative corrections.
They include the inner bremsstrahlung and contain a dependence of the beta
particle energy. In addition, they are discussed in terms of orders of
 , the fine structure constant. They originate from, for instance,
the emission of virtual photons by the final state charged particles. The zeroth
and the first order outer radiative corrections are shown in figure
, the fine structure constant. They originate from, for instance,
the emission of virtual photons by the final state charged particles. The zeroth
and the first order outer radiative corrections are shown in figure  .
In the course of the past two decades, radiative corrections of O(
.
In the course of the past two decades, radiative corrections of O( )
have been calculated as well as the leading terms of O(Z
)
have been calculated as well as the leading terms of O(Z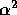 ) [Sir-87a].
The resulting radiative corrections (inner plus outer) amount to
) [Sir-87a].
The resulting radiative corrections (inner plus outer) amount to  with theoretical uncertainty of
with theoretical uncertainty of  arising mainly from
short-distance axial-vector-induced contributions [Mar-86].
arising mainly from
short-distance axial-vector-induced contributions [Mar-86].
The nucleus structure dependent corrections  are conventionally
factorized into two components: isospin impurity and radial overlap
corrections. The fact that
are conventionally
factorized into two components: isospin impurity and radial overlap
corrections. The fact that  is given by equation (
is given by equation ( )
rests on the assumption that the states involved are pure isospin states and
eigenstates of a charge independent hamiltonian. Even after accounting for
Coulomb interactions and spin-orbit coupling of the nucleus, the nuclear
force is still slightly charge dependent [Bli-73]. As a result, the nuclear
states involved in the decay are not pure isospin states. The radial overlap
corrections are due to small differences in the single-particle radial wave
functions of the neutron and the proton. Due to these differences, the radial
overlap integral of the parent and the daughter nucleus deviates from unity. The
evaluation of the isospin impurity correction is performed by adding an
isospin nonconserving (INC) interaction term to the standard shell-model
hamiltonian while the radial overlap correction is based on the radial wave
functions obtained from a suitable parametrization of the mean field.
There have been three systematic evaluations of
)
rests on the assumption that the states involved are pure isospin states and
eigenstates of a charge independent hamiltonian. Even after accounting for
Coulomb interactions and spin-orbit coupling of the nucleus, the nuclear
force is still slightly charge dependent [Bli-73]. As a result, the nuclear
states involved in the decay are not pure isospin states. The radial overlap
corrections are due to small differences in the single-particle radial wave
functions of the neutron and the proton. Due to these differences, the radial
overlap integral of the parent and the daughter nucleus deviates from unity. The
evaluation of the isospin impurity correction is performed by adding an
isospin nonconserving (INC) interaction term to the standard shell-model
hamiltonian while the radial overlap correction is based on the radial wave
functions obtained from a suitable parametrization of the mean field.
There have been three systematic evaluations of
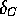 by Tower, Hardy and Harvey (THH) [Tow-77],
Wilkinson (W) [Wil-78] and Ormand and Brown (OB) [Orm-85] and [Orm-89].
The THH calculations of
by Tower, Hardy and Harvey (THH) [Tow-77],
Wilkinson (W) [Wil-78] and Ormand and Brown (OB) [Orm-85] and [Orm-89].
The THH calculations of  were carried out as follows: the radial
wave functions were obtained from a Woods-Saxon plus Coulomb potential and
the INC interaction term was determined by:
were carried out as follows: the radial
wave functions were obtained from a Woods-Saxon plus Coulomb potential and
the INC interaction term was determined by:
- adding Coulomb matrix elements to the proton-proton hamiltonian,
- increasing the
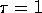 part of the proton-neutron interaction by
part of the proton-neutron interaction by  ,
,
- determining the single-particle energies from closed-core plus proton
and neutron nuclei [Orm-89].
On the other hand, the OB calculations of 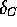 were based on an INC
interaction that was determined empirically by requiring that the parameters
of a Coulomb plus phenomenological isovector and isotensor potential reproduce
the experimental isotopic mass splittings. The OB radial wave functions were
obtained from a self-consistent Hartree-Fock calculation with a Skyrme-type
interaction which also included a Coulomb exchange term. The most recent and
theoretically refined is the OB calculation which yields a corrected
were based on an INC
interaction that was determined empirically by requiring that the parameters
of a Coulomb plus phenomenological isovector and isotensor potential reproduce
the experimental isotopic mass splittings. The OB radial wave functions were
obtained from a self-consistent Hartree-Fock calculation with a Skyrme-type
interaction which also included a Coulomb exchange term. The most recent and
theoretically refined is the OB calculation which yields a corrected
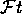 of
of  or
or  higher than that determined using THH
higher than that determined using THH
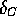 's.
's.
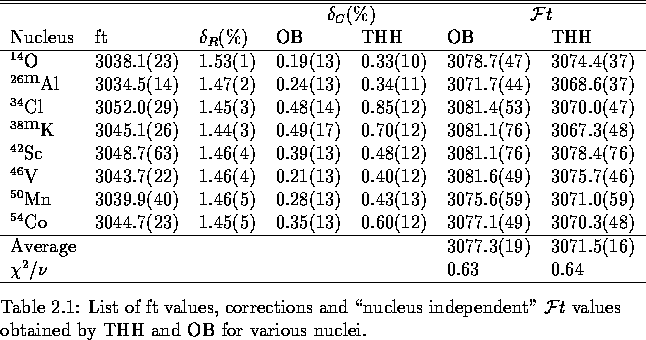
As shown in table  , both OB and THH values of
, both OB and THH values of 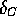 yield
essentially constant but inconsistent averaged
yield
essentially constant but inconsistent averaged  values.
The THH and OB nuclear corrections yield
values.
The THH and OB nuclear corrections yield 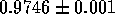 and
and  respectively for
respectively for  ; the errors quoted
are dominated by the uncertainties in
; the errors quoted
are dominated by the uncertainties in 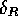 mentioned above.
Furthermore, considering the accepted value for
mentioned above.
Furthermore, considering the accepted value for  and
and 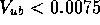 (
( confidence level), one gets for
confidence level), one gets for
 values of
values of 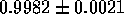 and
and
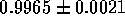 for THH and OB calculations respectively. The OB
calculations imply violation of CKM unitarity at the
for THH and OB calculations respectively. The OB
calculations imply violation of CKM unitarity at the  confidence level.
confidence level.
Recently, Drukarev and Strikman discovered that the  electron final
state interaction effects (Coulomb screening corrections) are more
pronounced than previously thought. This effect moves the central value of
electron final
state interaction effects (Coulomb screening corrections) are more
pronounced than previously thought. This effect moves the central value of
 away from unitarity.
away from unitarity.
Hardy et al. [Har-90] studied the spread of the THH and OB's 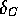 , did a
critical survey of available superallowed beta decay data and took unweighted
averages. As a result, Hardy et al. removed the discrepancy of THH and OB
calculations and reduced the overall uncertainties, bringing the unitarity test
to
, did a
critical survey of available superallowed beta decay data and took unweighted
averages. As a result, Hardy et al. removed the discrepancy of THH and OB
calculations and reduced the overall uncertainties, bringing the unitarity test
to
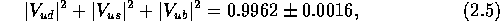
a value which is  lower than the Standard Model prediction.
lower than the Standard Model prediction.
From neutron beta decay,  can be extracted knowing the neutron lifetime
can be extracted knowing the neutron lifetime
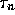 and
and  , the ratio of the weak axial vector to the vector
coupling constants. A new precision measurement of the electron asymmetry in
neutron decay [Ero-90] yields a new value for the ratio
, the ratio of the weak axial vector to the vector
coupling constants. A new precision measurement of the electron asymmetry in
neutron decay [Ero-90] yields a new value for the ratio
 . This result, combined with the average value of the
neutron lifetime,
. This result, combined with the average value of the
neutron lifetime, 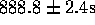 gives
gives  which leads to the unitarity test of
which leads to the unitarity test of
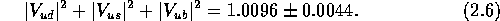
This value is higher than the Standard Model prediction by 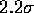 .
.
The pion beta decay, proceeding solely via the weak vector current interaction,
constitutes a superallowed transition from which  can be determined.
Given the discrepancy between the nuclear beta decay and the neutron beta decay
results discussed above, the determination of the pion beta decay rate at the
level of half a percent is of a clear importance and constitutes an independent
test of universality in the meson sector.
can be determined.
Given the discrepancy between the nuclear beta decay and the neutron beta decay
results discussed above, the determination of the pion beta decay rate at the
level of half a percent is of a clear importance and constitutes an independent
test of universality in the meson sector.
Contrary to nuclear beta decay, pion beta decay is free of the nuclear
overlap correction as well as the screening corrections. Sirlin [Sir-78]
has calculated the  decay rate taking into account the effects of
radiative corrections,
decay rate taking into account the effects of
radiative corrections,  which involve only an axial-vector
contribution [Mar-86].
which involve only an axial-vector
contribution [Mar-86].
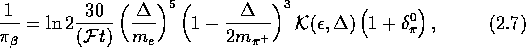
where

and

This result may be compared to the one obtained in chapter 4 without
radiative corrections.
This theoretical advantage of the pion beta decay is offset by experimental
difficulties. In fact, the main disavantage of the pion beta decay is its
small branching ratio  which makes it a very difficult process
to study with precision. The most precise measurements of the pion beta decay
rate to date are as follow:
which makes it a very difficult process
to study with precision. The most precise measurements of the pion beta decay
rate to date are as follow:
Using a stopped pion method, Depommier et al. [Dep-68] measured the branching
ratio for the pion beta decay at CERN. They observed  pion beta
events for
pion beta
events for 
 stopped in their apparatus. This led
to a decay rate of
stopped in their apparatus. This led
to a decay rate of  . Their result is in good
agreement with theory but the experimental error is too large for a significant
test of CVC.
. Their result is in good
agreement with theory but the experimental error is too large for a significant
test of CVC.
The most recent and most precise measurement of the  decay rate
is due to McFarlane et al. [McF-85] who performed an in-flight decay
measurement at LAMPF. Their result (
decay rate
is due to McFarlane et al. [McF-85] who performed an in-flight decay
measurement at LAMPF. Their result ( ), though
in good agreement with theoretical predictions
((
), though
in good agreement with theoretical predictions
(( ) is not precise enough (
) is not precise enough ( overall uncertainties) to test the full extent of the radiative corrections
which stand at
overall uncertainties) to test the full extent of the radiative corrections
which stand at  .
.
A precision determination of the pion beta decay rate is being carried
out in a two stage program at the Paul Scherrer Institute (PSI) in Switzerland.
The first phase of the
experiment is expected to yield a decay rate with an overall uncertainty of
 . At this level of precision, a test of CVC and the radiative
corrections will be possible. In addition, the superallowed Fermi decay data
could be compare to the neutron beta decay. The second stage of the experiment
will reduce the uncertainties still further to the level of
. At this level of precision, a test of CVC and the radiative
corrections will be possible. In addition, the superallowed Fermi decay data
could be compare to the neutron beta decay. The second stage of the experiment
will reduce the uncertainties still further to the level of  which
will test the CKM unitarity and constrain the following extensions
to the minimal Standard Model:
which
will test the CKM unitarity and constrain the following extensions
to the minimal Standard Model:
- The existence of a fourth generation of fermions which could be inferred
from an experimental violation of the CKM unitarity. At present, from the
nuclear Fermi decay data, an upper bound of
 (at
(at  confidence level)
is set on the mixing matrix element resulting from a fourth generation of
quarks.
confidence level)
is set on the mixing matrix element resulting from a fourth generation of
quarks.
- The existence of other gauge bosons
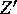 in addition to the known
in addition to the known
 and Z of electroweak theory. Marciano [Mar-87] and Sirlin [Sir-89]
have computed quantum loop corrections to the quark mixing angles resulting
from several types of
and Z of electroweak theory. Marciano [Mar-87] and Sirlin [Sir-89]
have computed quantum loop corrections to the quark mixing angles resulting
from several types of 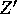 .
.
- Compositeness of fermions and gauge bosons which participate in weak
interactions. The experimental limits on the validity of quark-lepton
universality can be used to constrain the mass scale of compositeness.




Next: Pion Beam
Up: No Title
Previous: Superallowed Fermi Decay
Bernward Krause
Mon Jan 15 14:57:06 MET 1996
 ) is one of the fundamental
semileptonic weak interaction processes. It is a transition between two
spin-zero members of an isospin triplet and is therefore analogous to the
superallowed pure Fermi transitions in nuclear beta decay. At tree level,
the rate of pure Fermi nuclear beta decay is directly related to the vector
coupling constant
) is one of the fundamental
semileptonic weak interaction processes. It is a transition between two
spin-zero members of an isospin triplet and is therefore analogous to the
superallowed pure Fermi transitions in nuclear beta decay. At tree level,
the rate of pure Fermi nuclear beta decay is directly related to the vector
coupling constant  and the nuclear Fermi matrix element
and the nuclear Fermi matrix element  . The
Conserved Vector Current hypothesis (CVC) predicts that the product
ft of the Fermi integral function f and the decay half live
. The
Conserved Vector Current hypothesis (CVC) predicts that the product
ft of the Fermi integral function f and the decay half live 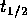 is a
universal constant given by:
is a
universal constant given by:






 to that of the muon decay, it is possible to determine
to that of the muon decay, it is possible to determine
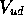 , the mixing matrix element between the u and d quarks.
Cabibbo universality relates
, the mixing matrix element between the u and d quarks.
Cabibbo universality relates  to the muon weak coupling constant
to the muon weak coupling constant
 via the CKM matrix element
via the CKM matrix element  [
[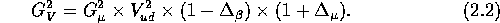
 is the muon decay coupling constant (see equation (
is the muon decay coupling constant (see equation ( and
and
 are the inner radiative corrections for
are the inner radiative corrections for  and
and
 decays respectively. The inner radiative corrections do not depend
on the electron energy. They do depend however on the details of the strong
interaction involved and the structure of the decay. In addition, they are
model-dependent and tend to diverge theoretically. They are relevant when
comparing different types of beta decay but act only to renormalize the
coupling constant when comparing the rates of beta decays of the same type.
In such cases, they are directly defined into the coupling constants themselves.
Some
decays respectively. The inner radiative corrections do not depend
on the electron energy. They do depend however on the details of the strong
interaction involved and the structure of the decay. In addition, they are
model-dependent and tend to diverge theoretically. They are relevant when
comparing different types of beta decay but act only to renormalize the
coupling constant when comparing the rates of beta decays of the same type.
In such cases, they are directly defined into the coupling constants themselves.
Some  nuclear beta decay processes, characterized
by the single parameter
nuclear beta decay processes, characterized
by the single parameter  are as follows:
are as follows:

 with
with  to the first excited state
of
to the first excited state
of  with
with  .
.
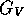 from the measured
decay rates: the phase
space dependent radiative corrections
from the measured
decay rates: the phase
space dependent radiative corrections  to the statistical
rate function f
to the statistical
rate function f  and the nuclear structure dependent
corrections
and the nuclear structure dependent
corrections  to the matrix element
to the matrix element 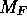
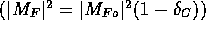 . The uncorrected Fermi matrix element
. The uncorrected Fermi matrix element
 is given by equation (
is given by equation ( and
and  and the matrix
element of equation (
and the matrix
element of equation (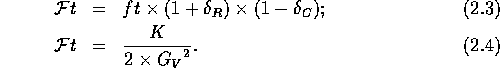
 are determined from the
are determined from the 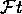 values.
values.
 are model-independent and uniquely
specified.
are model-independent and uniquely
specified.

 , the fine structure constant. They originate from, for instance,
the emission of virtual photons by the final state charged particles. The zeroth
and the first order outer radiative corrections are shown in figure
, the fine structure constant. They originate from, for instance,
the emission of virtual photons by the final state charged particles. The zeroth
and the first order outer radiative corrections are shown in figure  )
have been calculated as well as the leading terms of O(Z
)
have been calculated as well as the leading terms of O(Z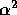 ) [
) [ with theoretical uncertainty of
with theoretical uncertainty of  arising mainly from
short-distance axial-vector-induced contributions [
arising mainly from
short-distance axial-vector-induced contributions [ are conventionally
factorized into two components: isospin impurity and radial overlap
corrections. The fact that
are conventionally
factorized into two components: isospin impurity and radial overlap
corrections. The fact that  is given by equation (
is given by equation (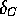 by Tower, Hardy and Harvey (THH) [
by Tower, Hardy and Harvey (THH) [ were carried out as follows: the radial
wave functions were obtained from a Woods-Saxon plus Coulomb potential and
the INC interaction term was determined by:
were carried out as follows: the radial
wave functions were obtained from a Woods-Saxon plus Coulomb potential and
the INC interaction term was determined by:
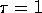 part of the proton-neutron interaction by
part of the proton-neutron interaction by  ,
,
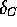 were based on an INC
interaction that was determined empirically by requiring that the parameters
of a Coulomb plus phenomenological isovector and isotensor potential reproduce
the experimental isotopic mass splittings. The OB radial wave functions were
obtained from a self-consistent Hartree-Fock calculation with a Skyrme-type
interaction which also included a Coulomb exchange term. The most recent and
theoretically refined is the OB calculation which yields a corrected
were based on an INC
interaction that was determined empirically by requiring that the parameters
of a Coulomb plus phenomenological isovector and isotensor potential reproduce
the experimental isotopic mass splittings. The OB radial wave functions were
obtained from a self-consistent Hartree-Fock calculation with a Skyrme-type
interaction which also included a Coulomb exchange term. The most recent and
theoretically refined is the OB calculation which yields a corrected
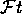 of
of  or
or  higher than that determined using THH
higher than that determined using THH
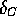 's.
's.

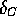 yield
essentially constant but inconsistent averaged
yield
essentially constant but inconsistent averaged  values.
The THH and OB nuclear corrections yield
values.
The THH and OB nuclear corrections yield 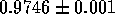 and
and  respectively for
respectively for  ; the errors quoted
are dominated by the uncertainties in
; the errors quoted
are dominated by the uncertainties in 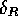 mentioned above.
Furthermore, considering the accepted value for
mentioned above.
Furthermore, considering the accepted value for  and
and 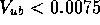 (
( confidence level), one gets for
confidence level), one gets for
 values of
values of 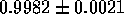 and
and
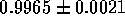 for THH and OB calculations respectively. The OB
calculations imply violation of CKM unitarity at the
for THH and OB calculations respectively. The OB
calculations imply violation of CKM unitarity at the  confidence level.
confidence level.
 electron final
state interaction effects (Coulomb screening corrections) are more
pronounced than previously thought. This effect moves the central value of
electron final
state interaction effects (Coulomb screening corrections) are more
pronounced than previously thought. This effect moves the central value of
 away from unitarity.
away from unitarity.
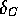 , did a
critical survey of available superallowed beta decay data and took unweighted
averages. As a result, Hardy et al. removed the discrepancy of THH and OB
calculations and reduced the overall uncertainties, bringing the unitarity test
to
, did a
critical survey of available superallowed beta decay data and took unweighted
averages. As a result, Hardy et al. removed the discrepancy of THH and OB
calculations and reduced the overall uncertainties, bringing the unitarity test
to
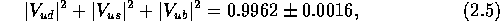
 lower than the Standard Model prediction.
lower than the Standard Model prediction.
 can be extracted knowing the neutron lifetime
can be extracted knowing the neutron lifetime
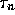 and
and  , the ratio of the weak axial vector to the vector
coupling constants. A new precision measurement of the electron asymmetry in
neutron decay [
, the ratio of the weak axial vector to the vector
coupling constants. A new precision measurement of the electron asymmetry in
neutron decay [ . This result, combined with the average value of the
neutron lifetime,
. This result, combined with the average value of the
neutron lifetime, 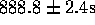 gives
gives  which leads to the unitarity test of
which leads to the unitarity test of
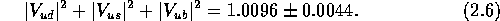
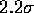 .
.
 can be determined.
Given the discrepancy between the nuclear beta decay and the neutron beta decay
results discussed above, the determination of the pion beta decay rate at the
level of half a percent is of a clear importance and constitutes an independent
test of universality in the meson sector.
can be determined.
Given the discrepancy between the nuclear beta decay and the neutron beta decay
results discussed above, the determination of the pion beta decay rate at the
level of half a percent is of a clear importance and constitutes an independent
test of universality in the meson sector.
 decay rate taking into account the effects of
radiative corrections,
decay rate taking into account the effects of
radiative corrections,  which involve only an axial-vector
contribution [
which involve only an axial-vector
contribution [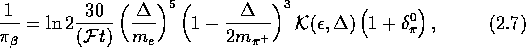


 which makes it a very difficult process
to study with precision. The most precise measurements of the pion beta decay
rate to date are as follow:
which makes it a very difficult process
to study with precision. The most precise measurements of the pion beta decay
rate to date are as follow:
 pion beta
events for
pion beta
events for 
 stopped in their apparatus. This led
to a decay rate of
stopped in their apparatus. This led
to a decay rate of  . Their result is in good
agreement with theory but the experimental error is too large for a significant
test of CVC.
. Their result is in good
agreement with theory but the experimental error is too large for a significant
test of CVC.
 decay rate
is due to McFarlane et al. [
decay rate
is due to McFarlane et al. [ ), though
in good agreement with theoretical predictions
((
), though
in good agreement with theoretical predictions
(( ) is not precise enough (
) is not precise enough ( overall uncertainties) to test the full extent of the radiative corrections
which stand at
overall uncertainties) to test the full extent of the radiative corrections
which stand at  .
.
 . At this level of precision, a test of CVC and the radiative
corrections will be possible. In addition, the superallowed Fermi decay data
could be compare to the neutron beta decay. The second stage of the experiment
will reduce the uncertainties still further to the level of
. At this level of precision, a test of CVC and the radiative
corrections will be possible. In addition, the superallowed Fermi decay data
could be compare to the neutron beta decay. The second stage of the experiment
will reduce the uncertainties still further to the level of  which
will test the CKM unitarity and constrain the following extensions
to the minimal Standard Model:
which
will test the CKM unitarity and constrain the following extensions
to the minimal Standard Model:
 (at
(at  confidence level)
is set on the mixing matrix element resulting from a fourth generation of
quarks.
confidence level)
is set on the mixing matrix element resulting from a fourth generation of
quarks.
 in addition to the known
in addition to the known
 and Z of electroweak theory. Marciano [
and Z of electroweak theory. Marciano [ .
.