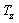
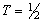
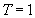
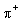
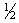
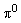
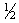
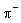






The pion-nucleon system represents a linear combination of isospin T=3/2 and T=1/2 isospin states, since nucleons form an isospin 1/2 doublet and pions an isospin 1 triplet, which are broken by electric charge. The third isospin component Tz is attributed to the discussed particles as follows:
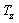
|
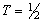
|
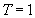
|
| 1
|
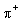
| |
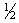
|
p
|
|
| 0
|
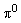
| |
-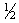
|
n
|
|
| -1
|
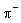
|
In combination they form either one of four T3/2 or two T1/2 states, where only the Tz = ±3/2 orientation directly can be attributed to
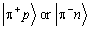 ,
respectively.
,
respectively.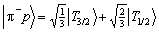
and
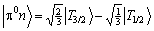 ,
,
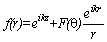 ,
,where q represents the scattering angle. Or in a different form (following [Che57]), when the pion wavefunction is denoted as p (q):
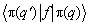 ,
,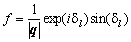 .
.As is well known the differential cross section is given by d s /d W =F(q',q)2. It is useful to perform a partial wave decomposition. Then F becomes
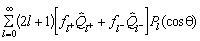 ,
where
,
where
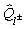
Since the pion is captured at rest we can neglect all orbital momenta other than l=0 (s-waves). So
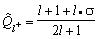 becomes 1 and
becomes 1 and
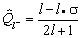 0;
0;s is the pion spin position. In addition one should take the isospin decomposition into account and make use of the isospin projection operators
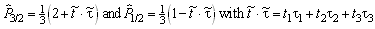 ,
,
Thus,
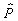 projects the total isospin T=1/2 and T=3/2 states out of the
p N system. For example:
projects the total isospin T=1/2 and T=3/2 states out of the
p N system. For example:
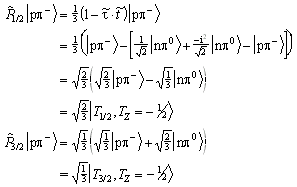 .
.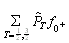 ,
since
,
since
 .
.In the case of - elastic scattering one obtains
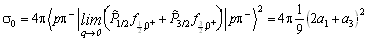
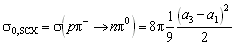 ,
,
having denoted the scattering lengths a1 for T=1/2 and
a3 for T=3/2. Often
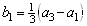 is used, as well.
is used, as well.
 ,
, only
only
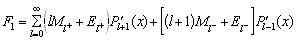
contributes [Che57]. With l representing orbital angular momentum
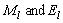 are the magnetic and electric transition amplitudes, respectively. Then the
differential cross section becomes
are the magnetic and electric transition amplitudes, respectively. Then the
differential cross section becomes
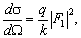
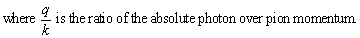 Due to the p3 momentum dependence of the p-wave amplitudes
(p5 for E2-, respectively) only the s-wave term is
significant in our case, since the is captured at rest. This leads to
Due to the p3 momentum dependence of the p-wave amplitudes
(p5 for E2-, respectively) only the s-wave term is
significant in our case, since the is captured at rest. This leads to
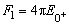 .
.Then , the threshold amplitude of pion photoproduction, is defined via
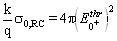 [Kov97].
[Kov97].
Hence, the electric dipole amplitude
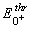 with
l p =0 and total spin j=1/2 fully describes the pion
photoproduction cross section (and therefore the radiative capture, as well).
The ratio of the fundamental processes for a stopping in a H-nucleus then
consistently is given through s-wave pion scattering at threshold and
calculates to
with
l p =0 and total spin j=1/2 fully describes the pion
photoproduction cross section (and therefore the radiative capture, as well).
The ratio of the fundamental processes for a stopping in a H-nucleus then
consistently is given through s-wave pion scattering at threshold and
calculates to
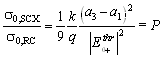 .
.
Hence, knowing
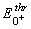 ,
the p N scattering length b1 can be obtained directly by
measuring the Panofsky ratio.
,
the p N scattering length b1 can be obtained directly by
measuring the Panofsky ratio.
Using
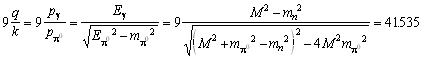
and P=1.546 [Spu77], the actual value is
-0.253/m p .
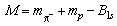 has been used with the correction for the binding energy of pionic hydrogen
B1s=0.00324 MeV.
has been used with the correction for the binding energy of pionic hydrogen
B1s=0.00324 MeV.





